Skip to main content

运用递归解决二叉树的问题

· 8 min read

总结一下递归解决二叉树问题的思考方向

前言​

递归是树的特性之一也是解决树的相关问题最有效和最常用的方法之一，许多树问题可以通过递归的方式来解决。 对于每个递归层级，我们只能关注单个节点内的问题，并通过递归调用函数来解决其子节点问题。

通常有两个思考方向：

  • 自顶向下
  • 自底向上

自顶向下思路​

“自顶向下” 意味着在每个递归层级，我们将首先访问节点来计算一些值，并在递归调用函数时将这些值传递到下一个子节点。 所以 “自顶向下” 的解决方案可以被认为是一种前序遍历。

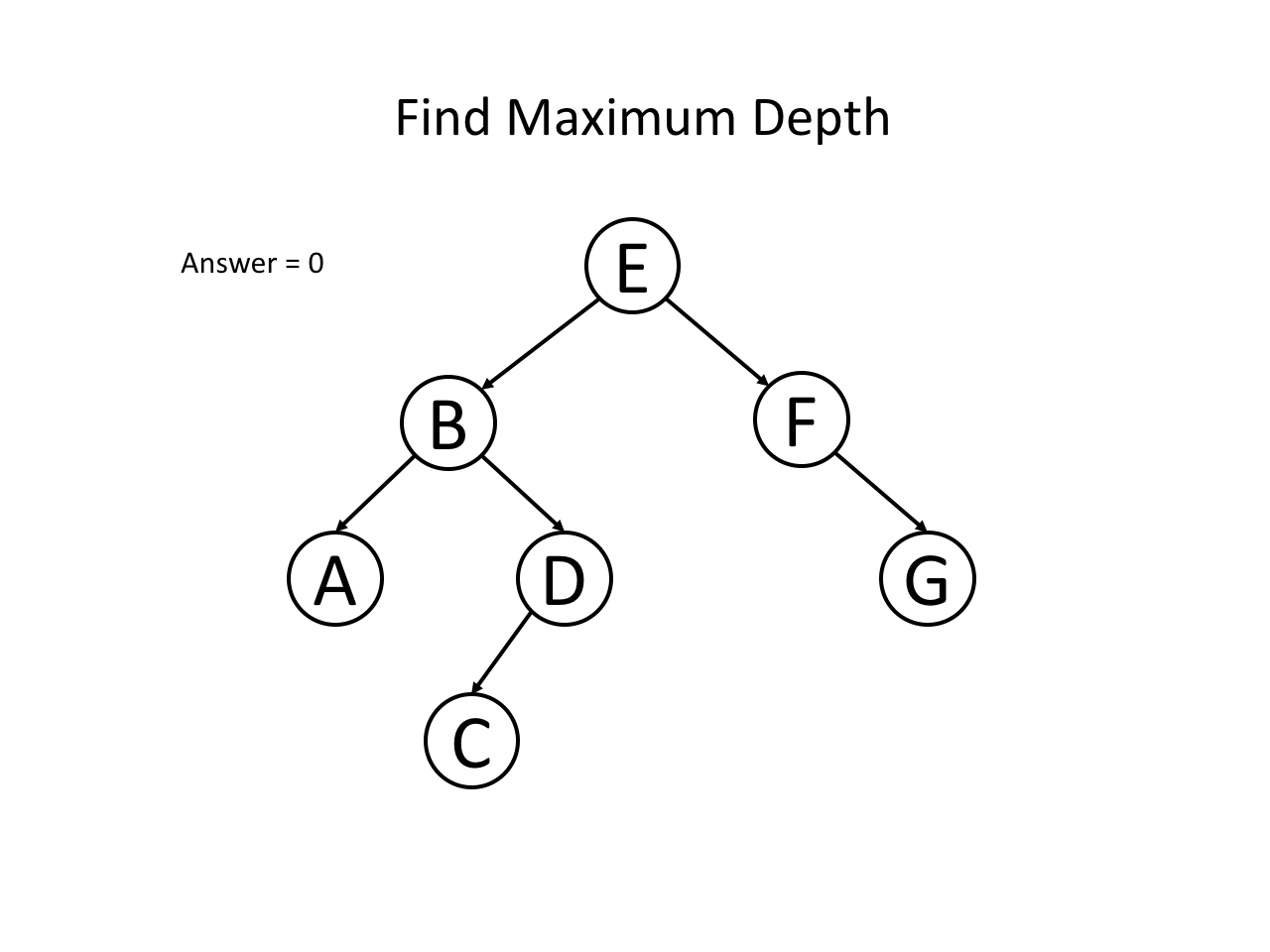
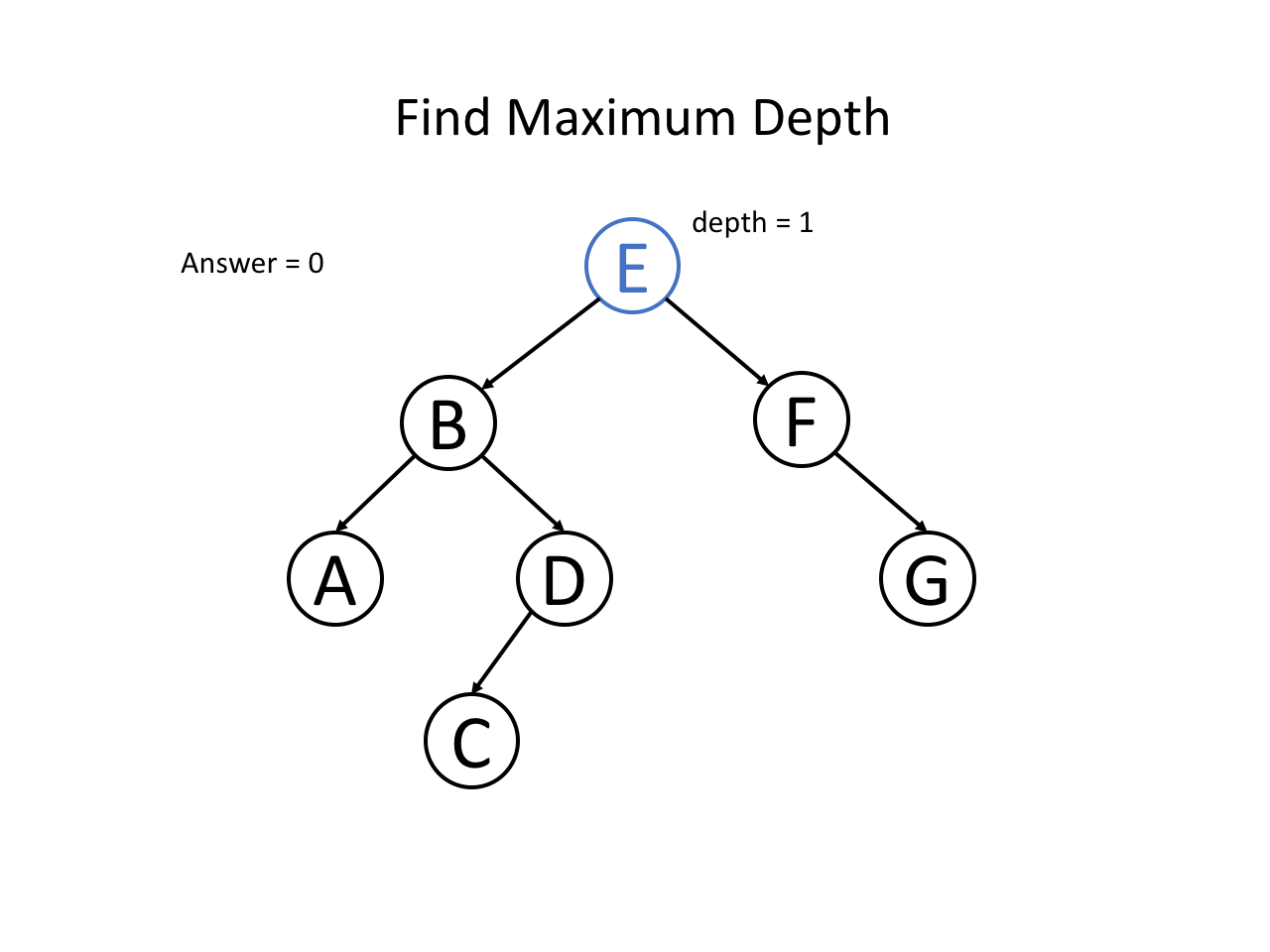
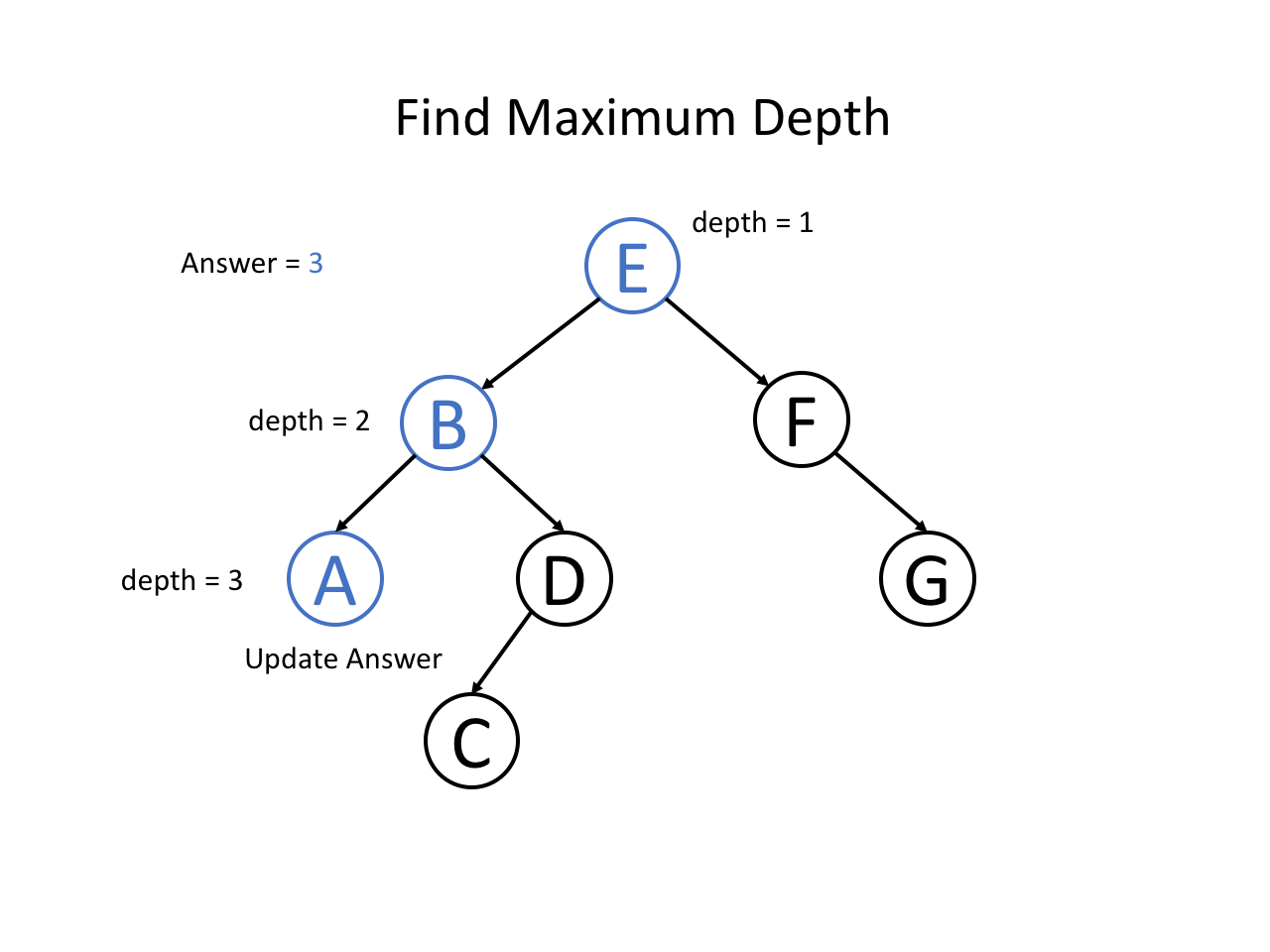
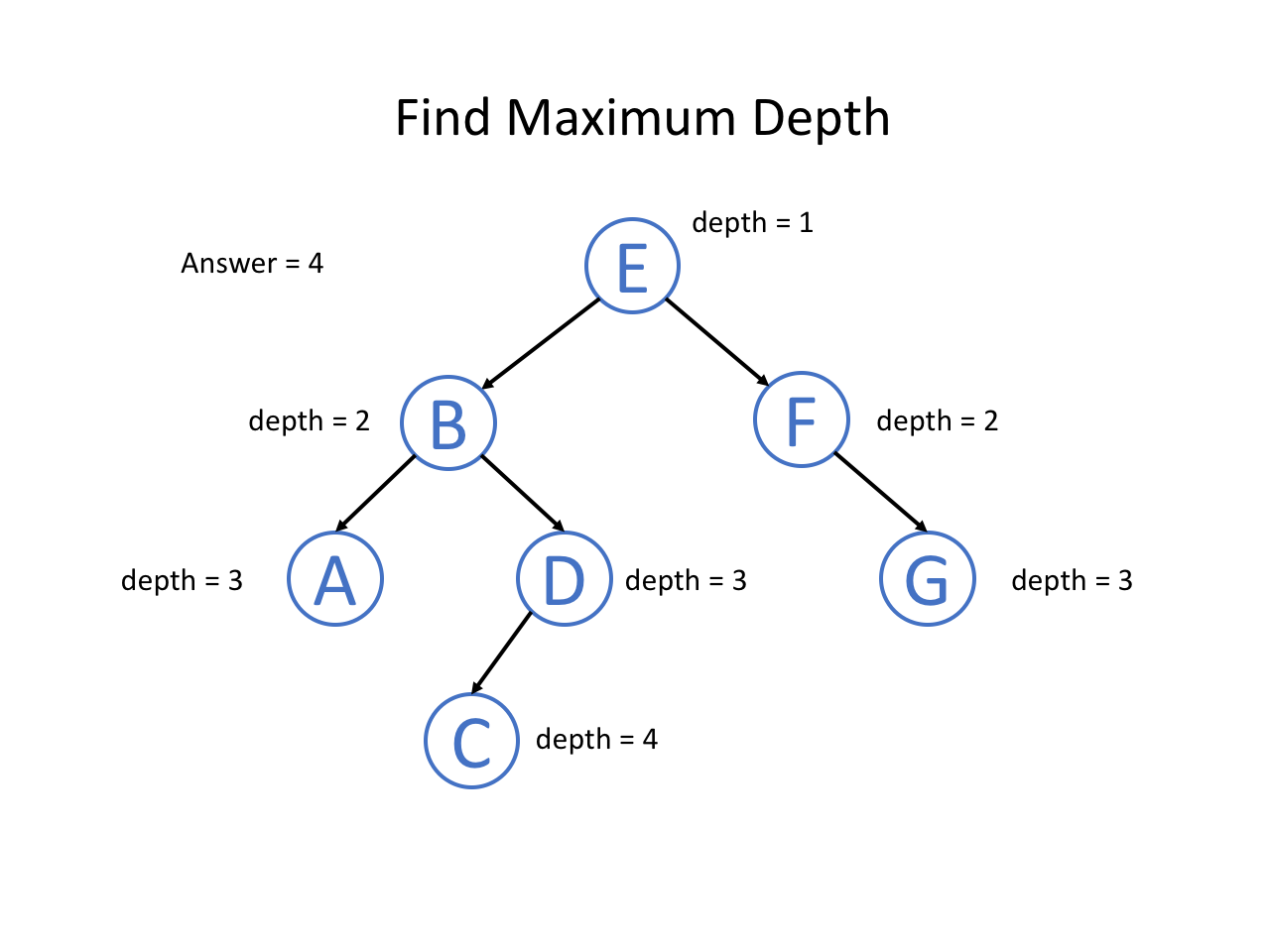
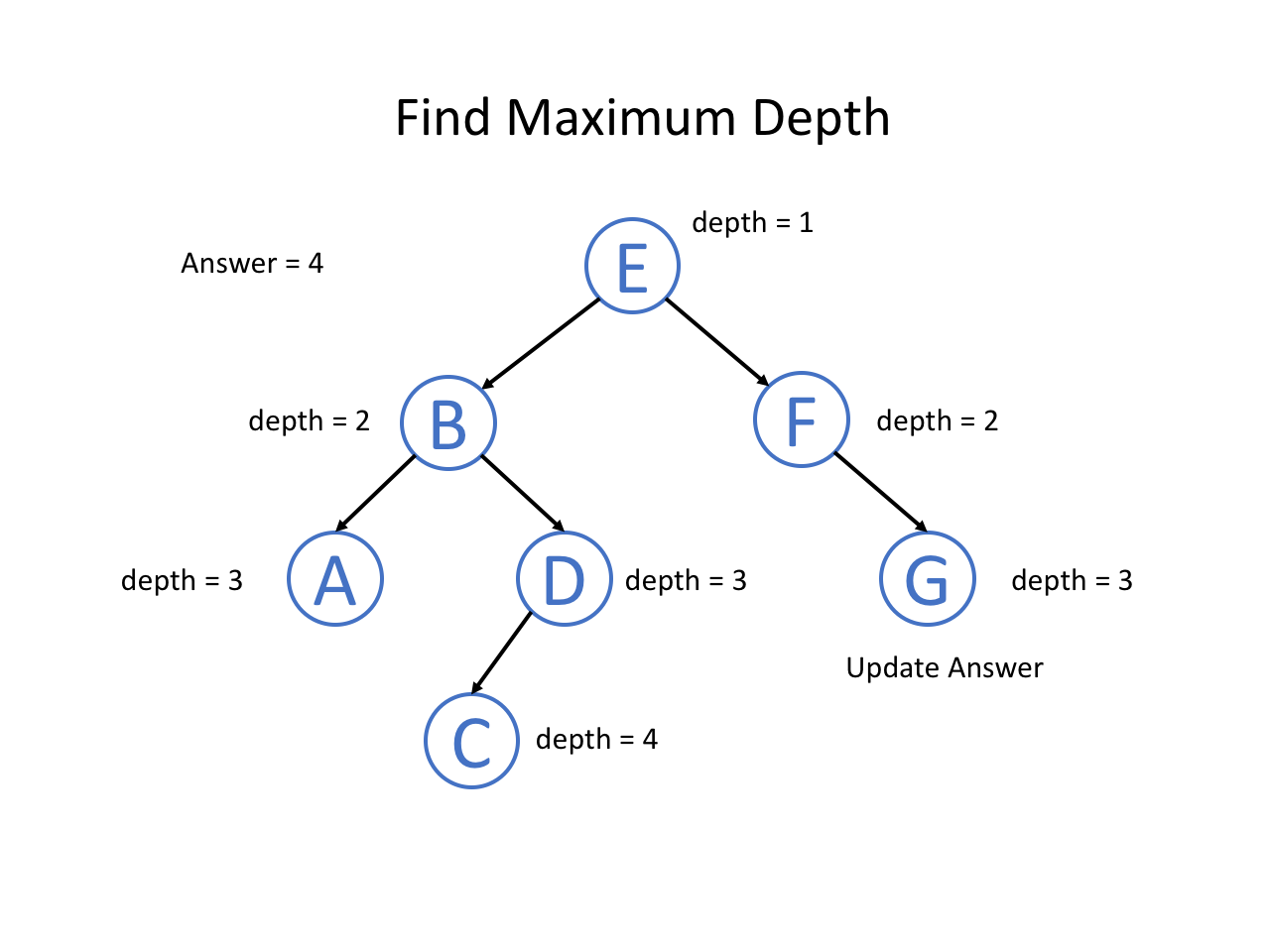
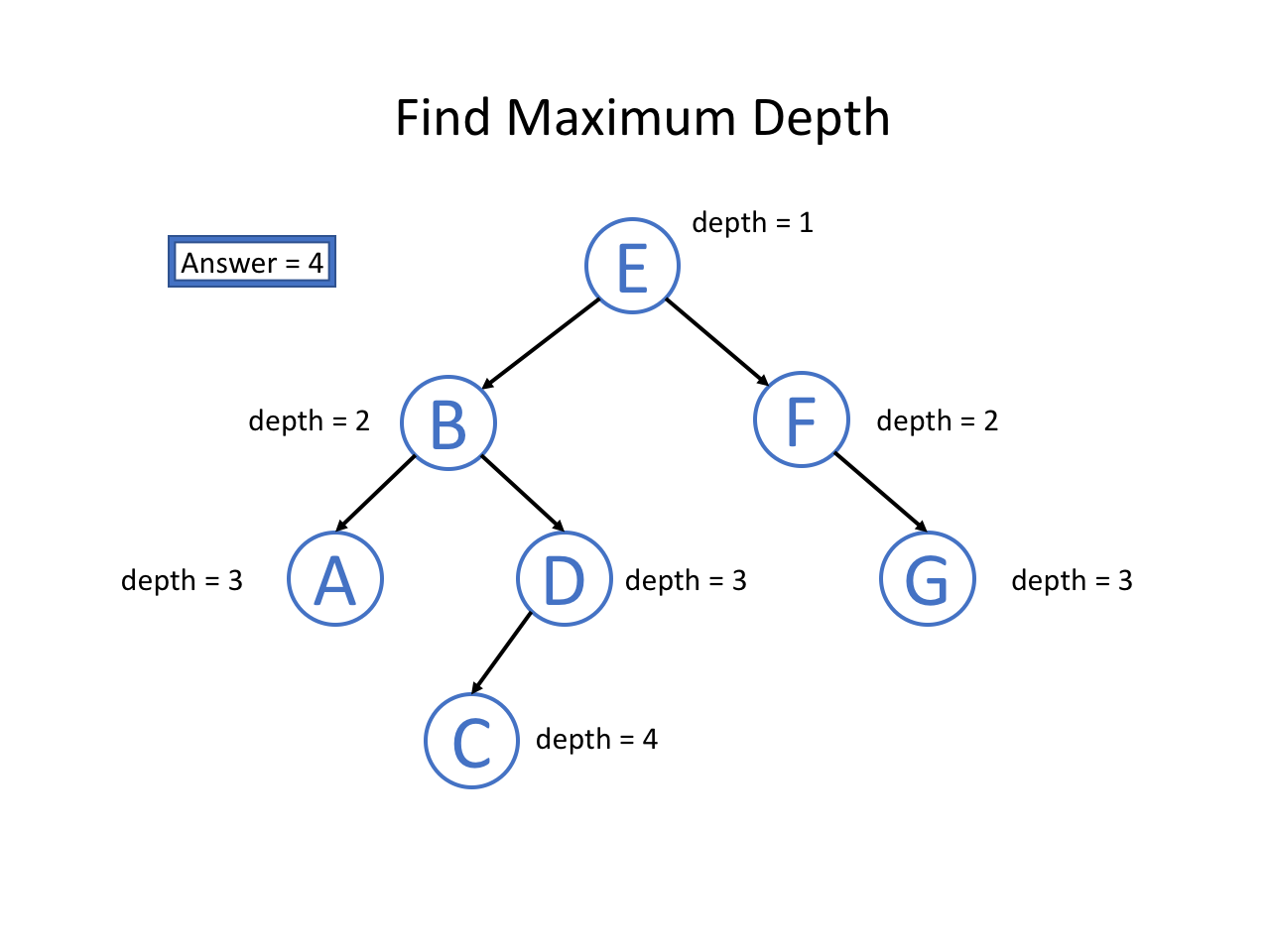
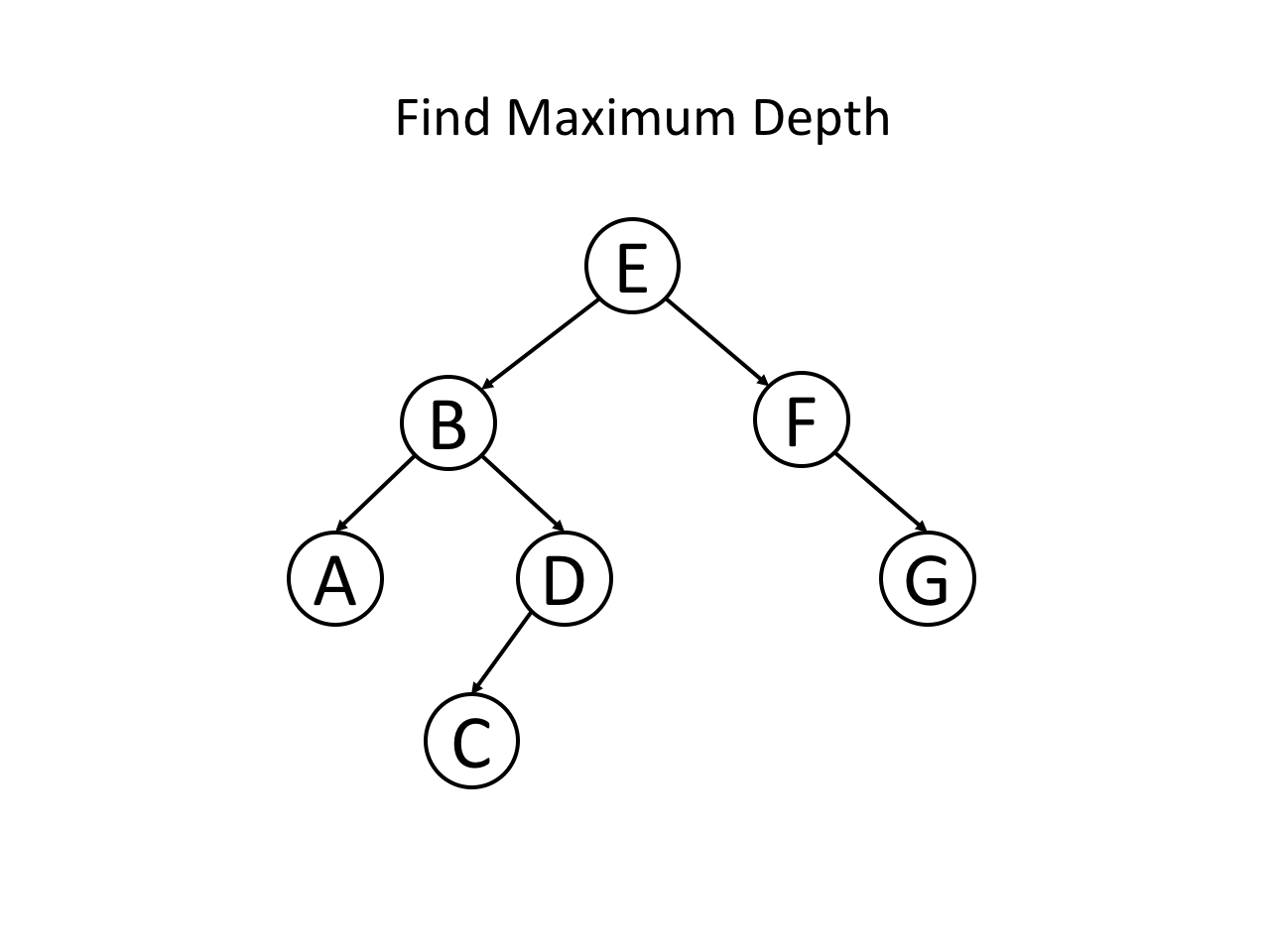
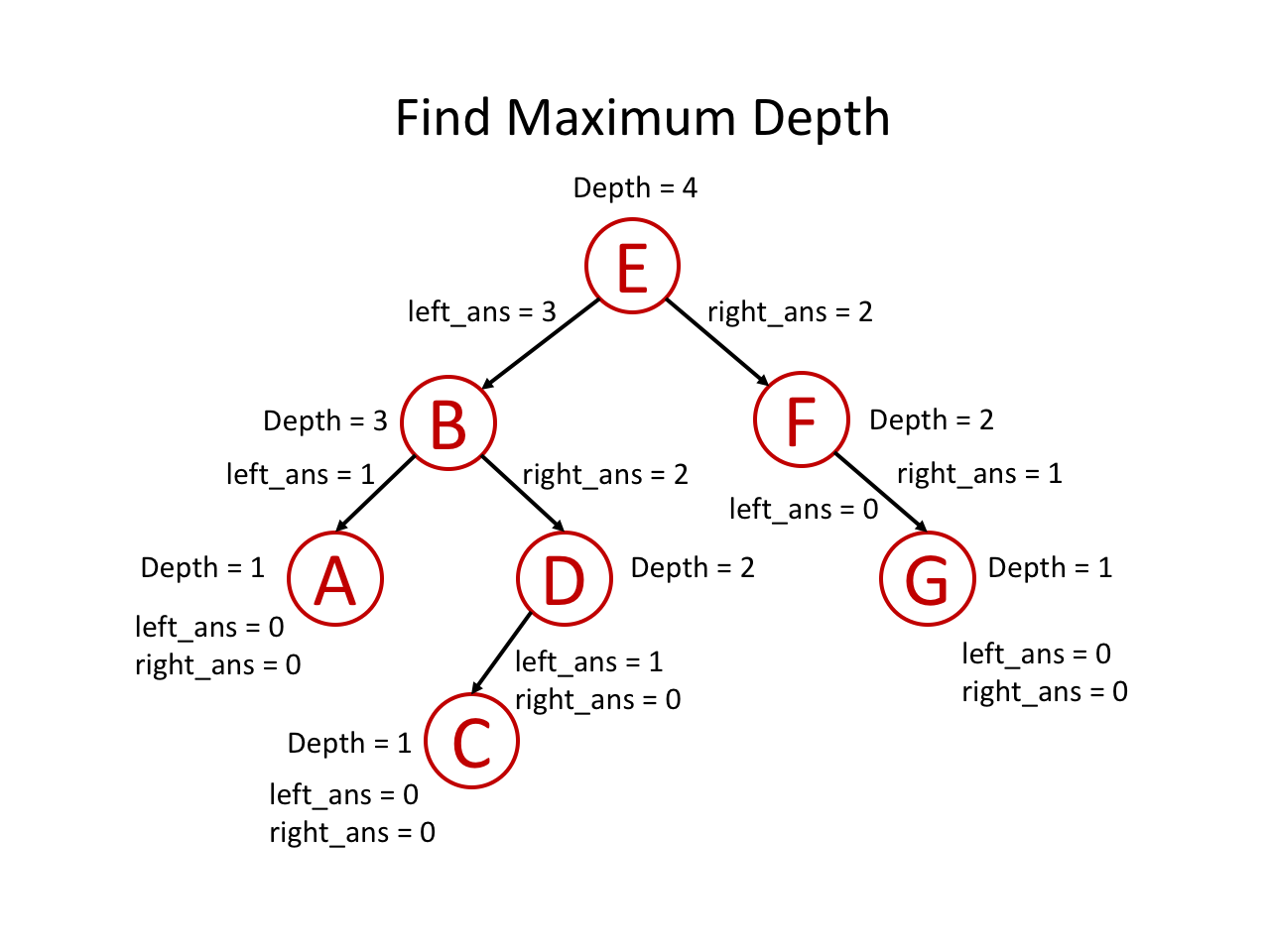
下面，我们通过自顶向下的思路分析一道题：二叉树的最大深度

题意是找到一棵二叉树的最大深度是多少，即从根节点到叶子节点的最大层数是多少。

确定递归参数​

由于是使用自顶向下的思路，我们就需要从根节点出发，进行深度优先搜索，每到下一个节点就需要知道该节点所在层数是多少，所以 dfs 递归函数中：

  • 第一个参数表示二叉树中的某个节点
  • 第二个参数表示该节点所在层数
function dfs(root, depth) {}

回归定义找到递归终止条件​

当 root 为 null 时就直接返回该层函数调用，回溯到上一个状态。

function dfs(root, depth) {
  if (!root) return;
}

确定每一层递归要做的事情​

  • 判断该节点是否为叶子节点，如果是叶子节点则更新 ans
  • 递归进入左子树和右子树，每次递归 depth 参数 + 1
function dfs(root, depth) {
  if (!root) return;

  // 判断是否是叶子节点
  if (!root.left && !root.right) ans = Math.max(ans, depth);

  // 递归左子树和右子树
  dfs(root.right, depth + 1);
  dfs(root.left, depth + 1);
}

最终代码​

function maxDepth(root) {
  let ans = 0;
  dfs(root, 1);

  function dfs(root, depth) {
    if (!root) return;
    if (!root.left && !root.right) ans = Math.max(ans, depth);

    dfs(root.left, depth + 1);
    dfs(root.right, depth + 1);
  }

  return ans;
}

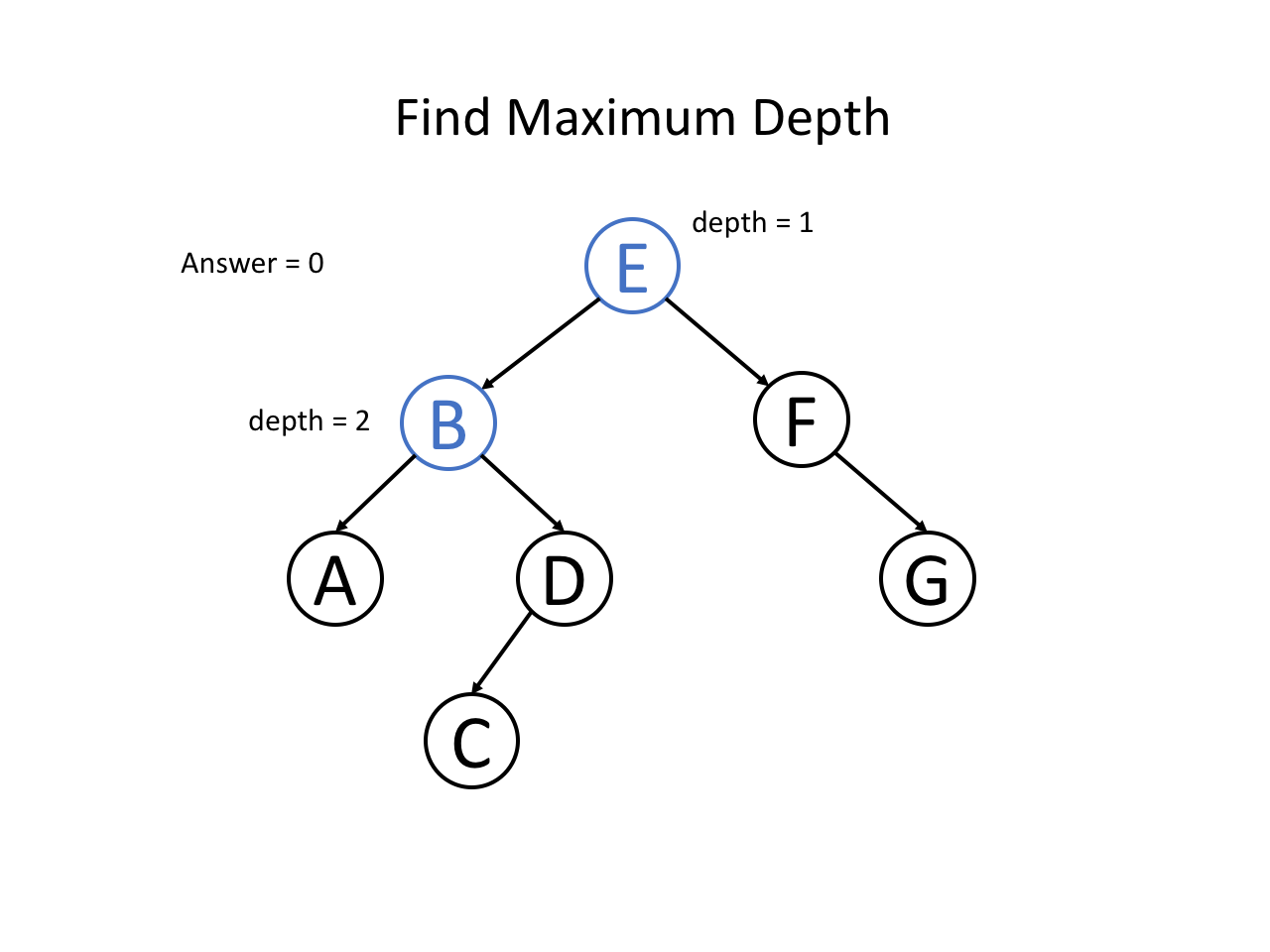
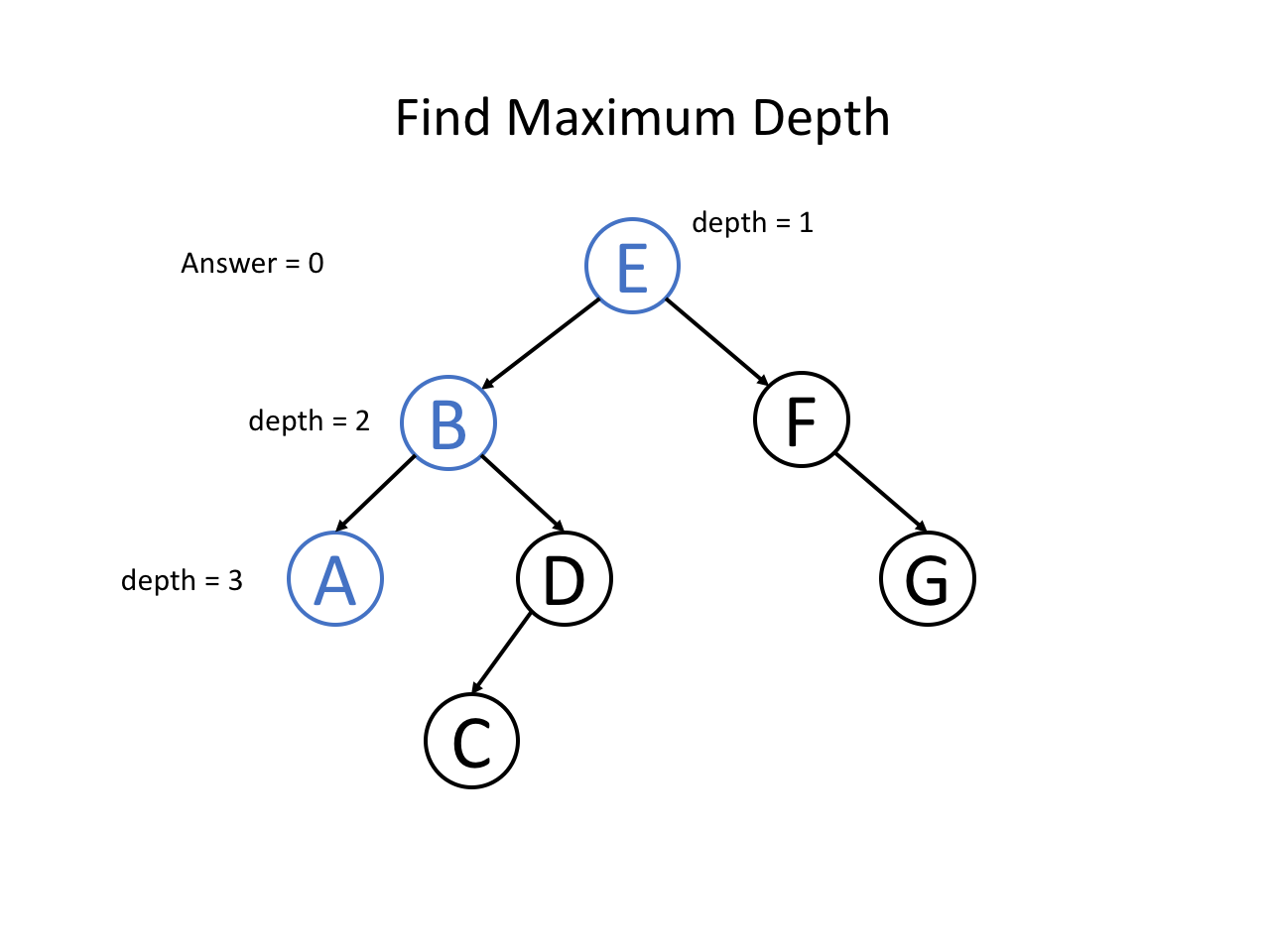
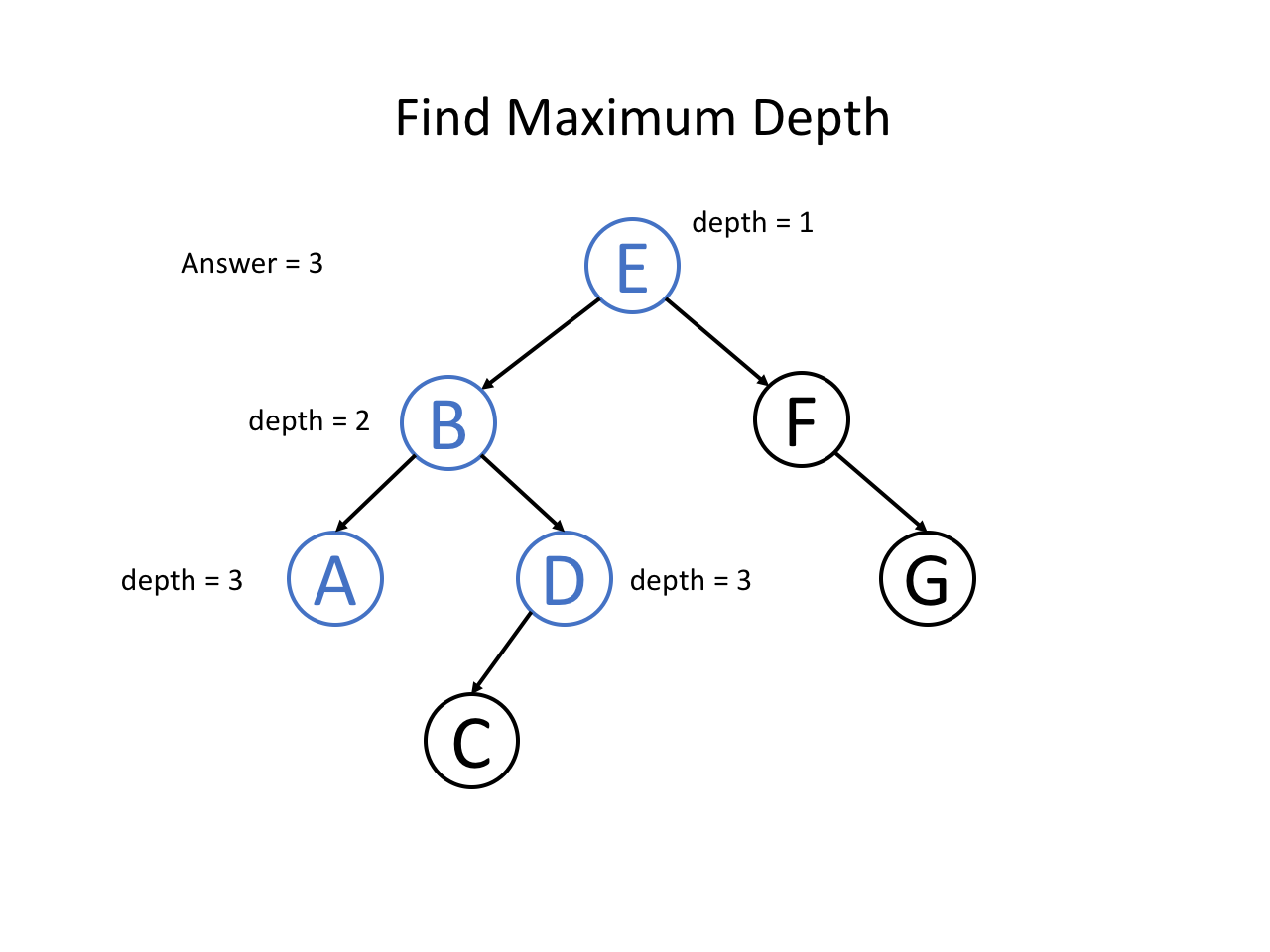
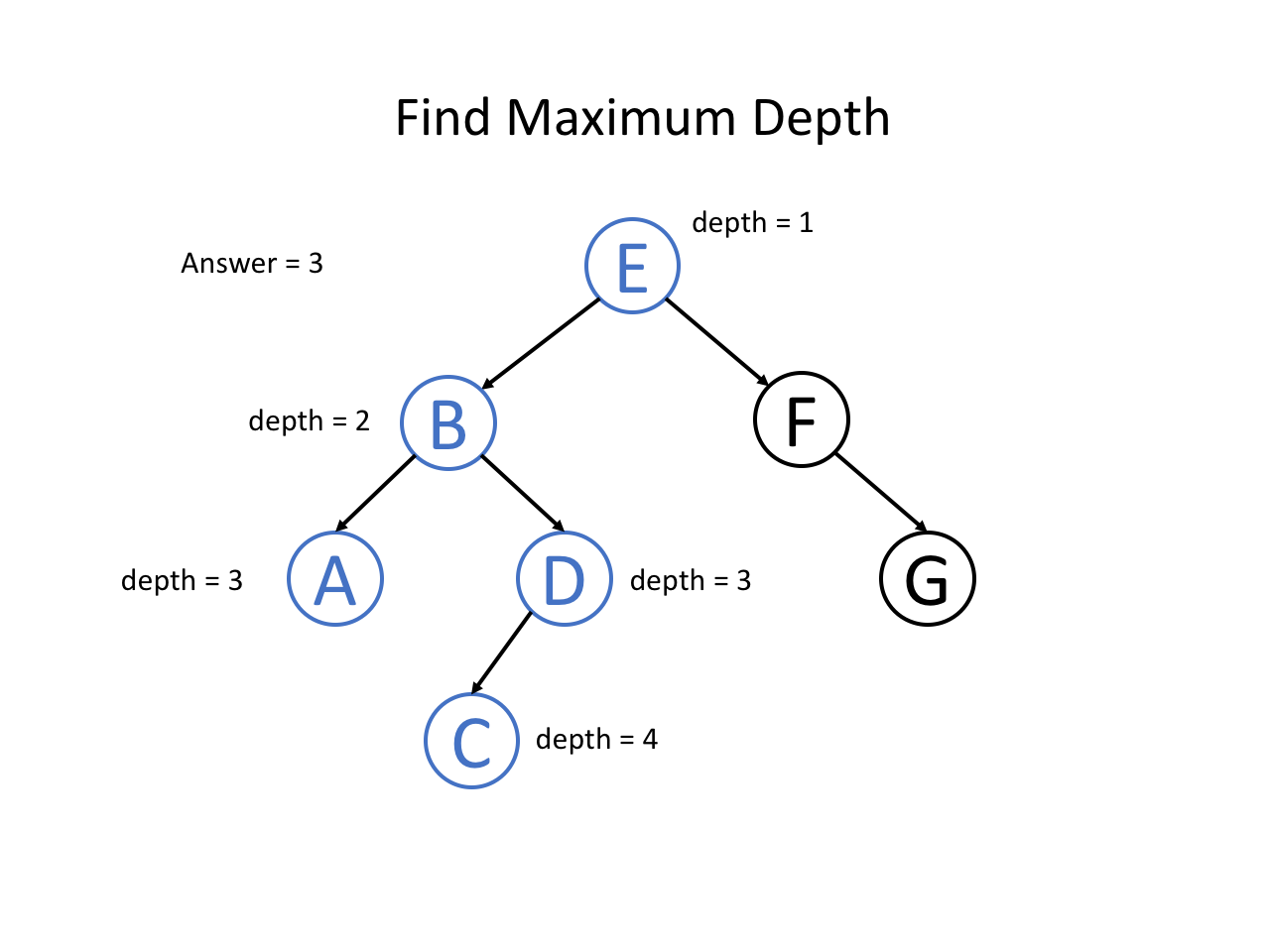
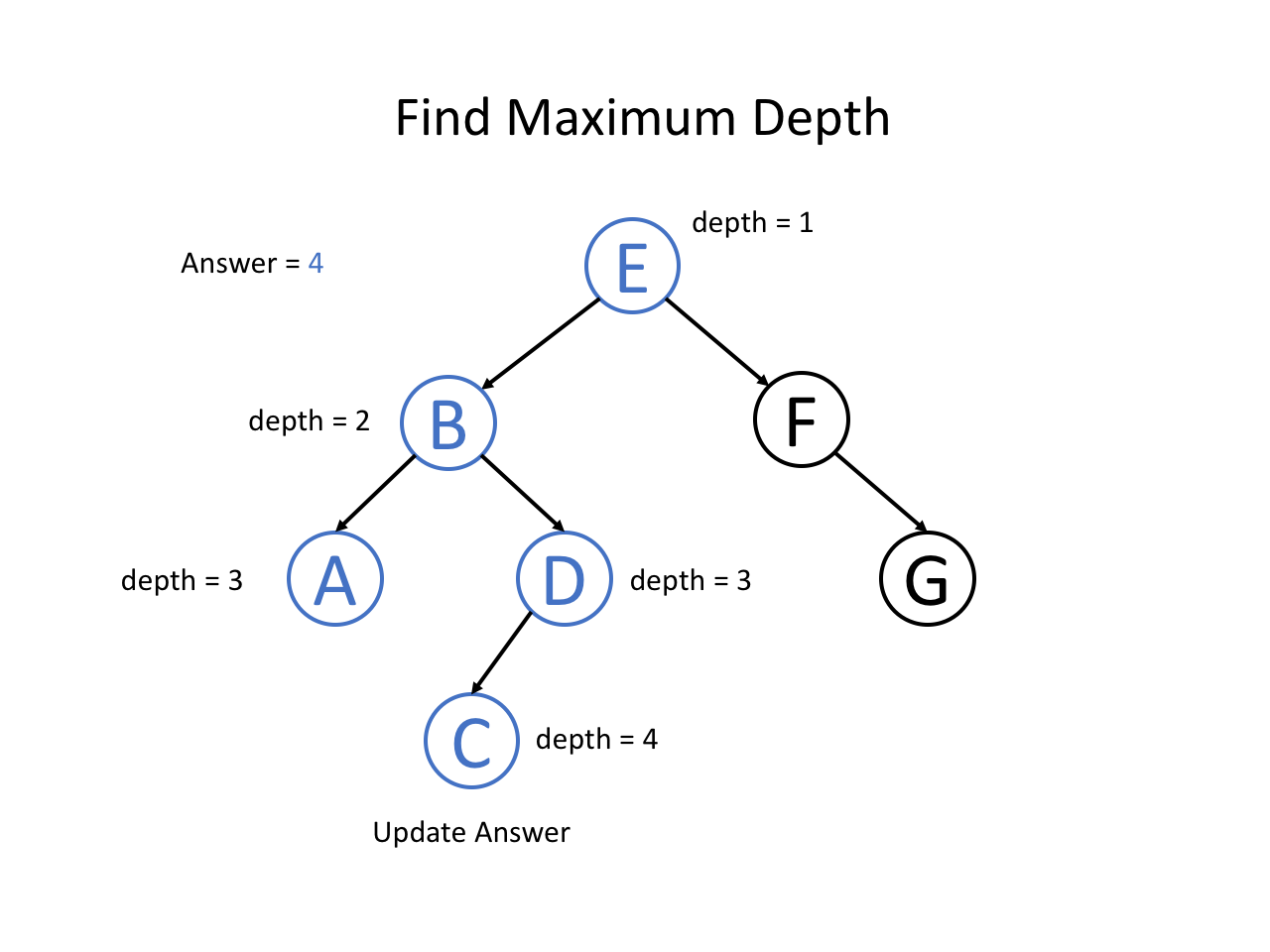
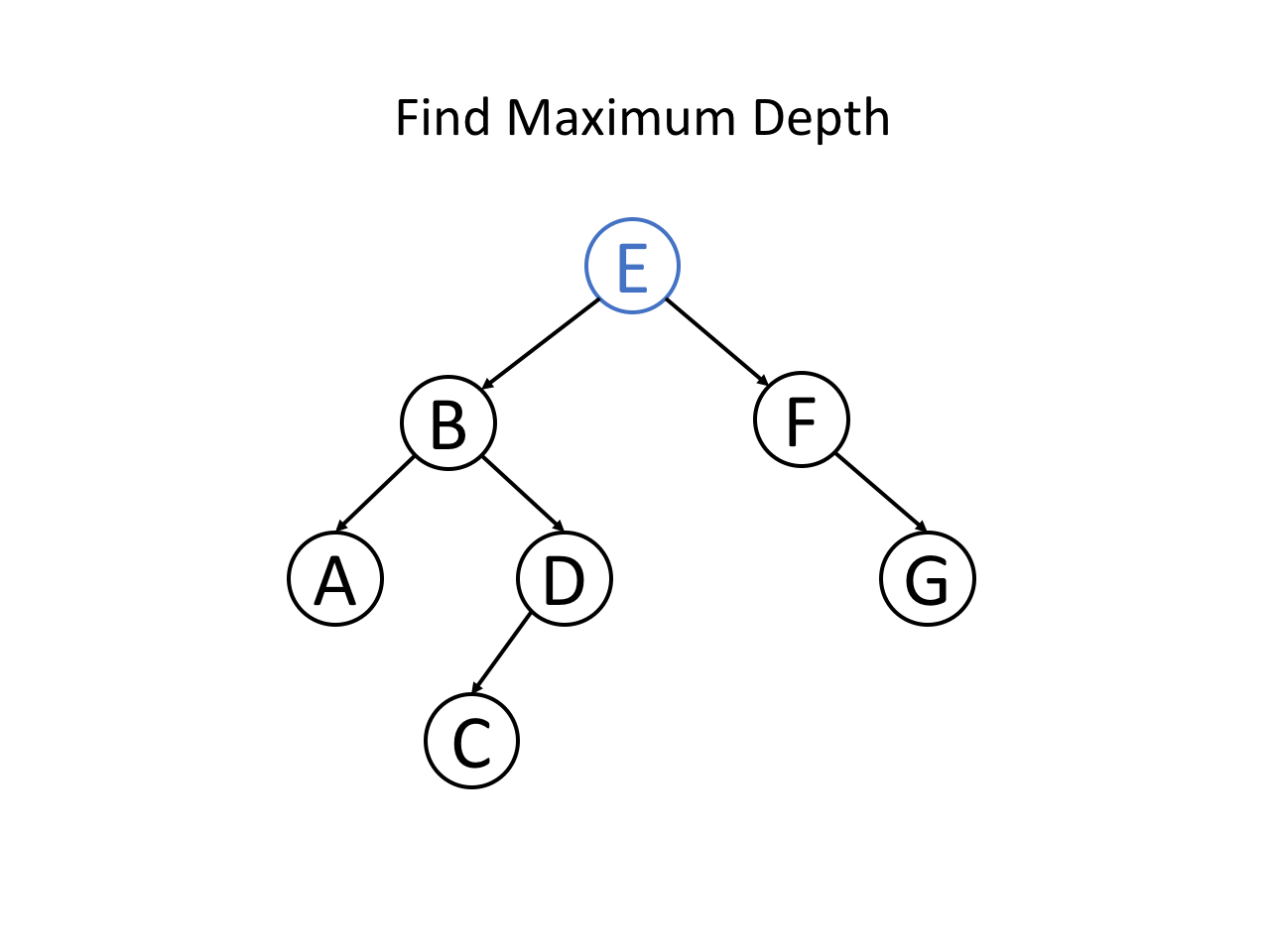
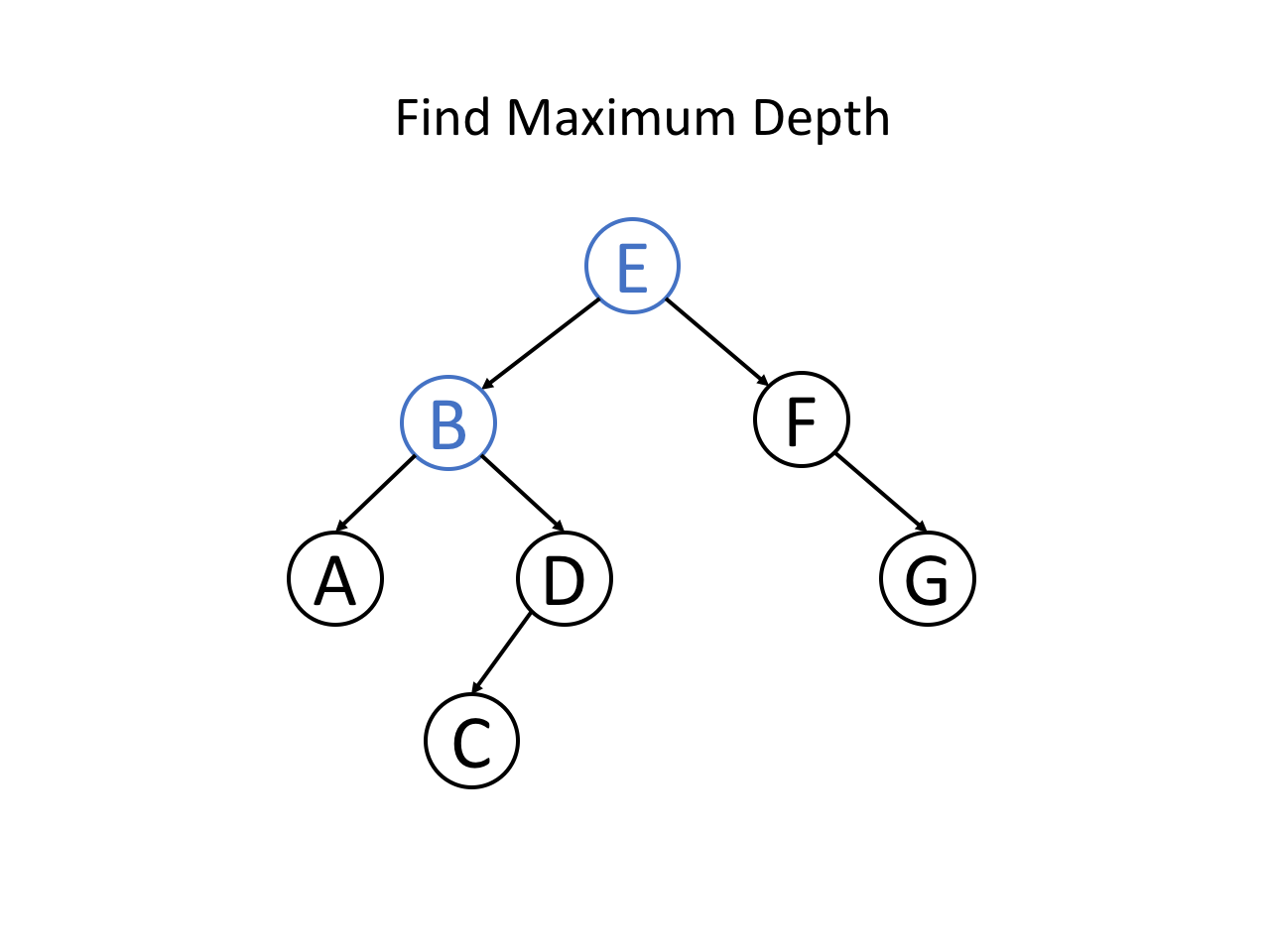
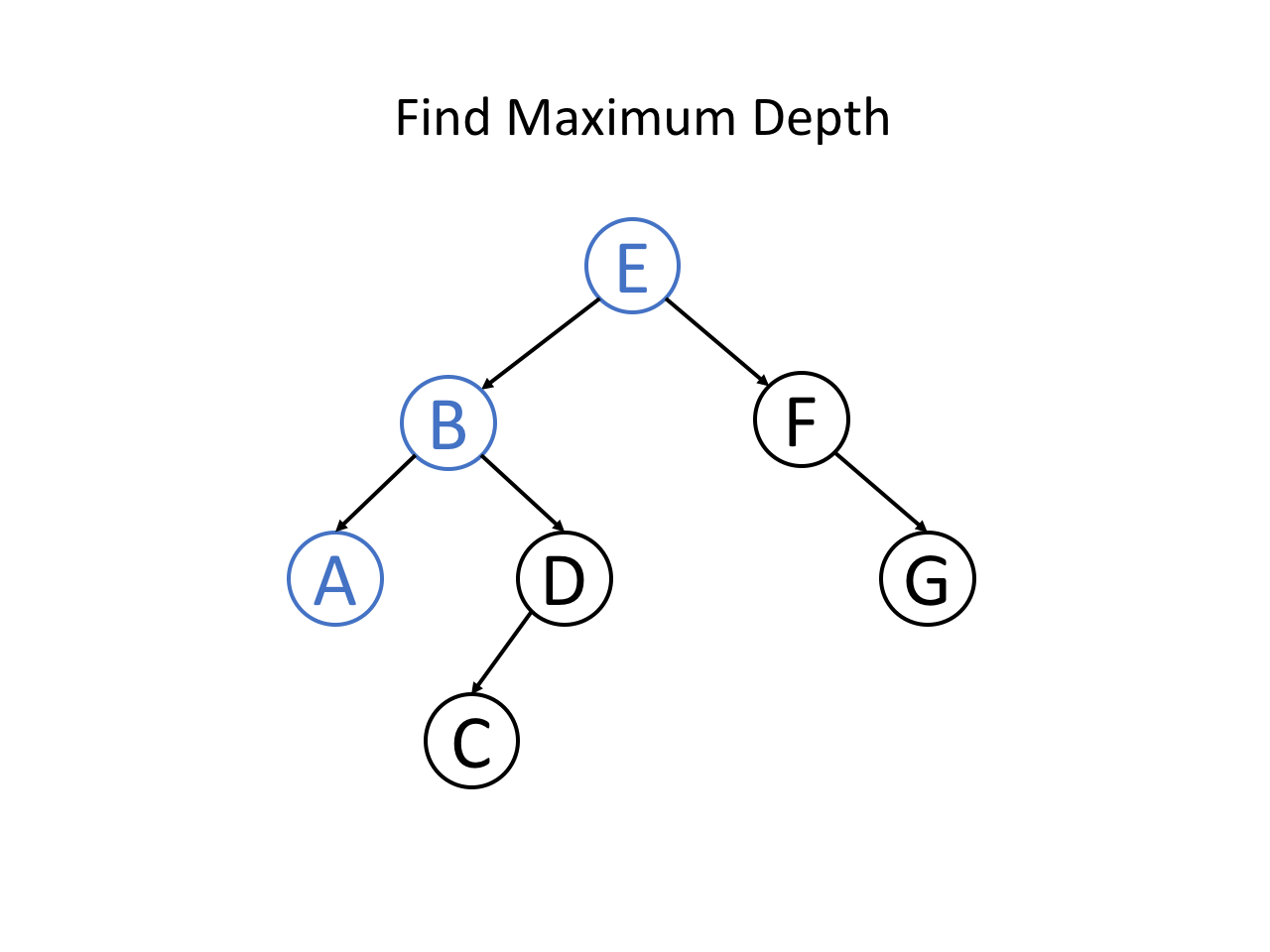
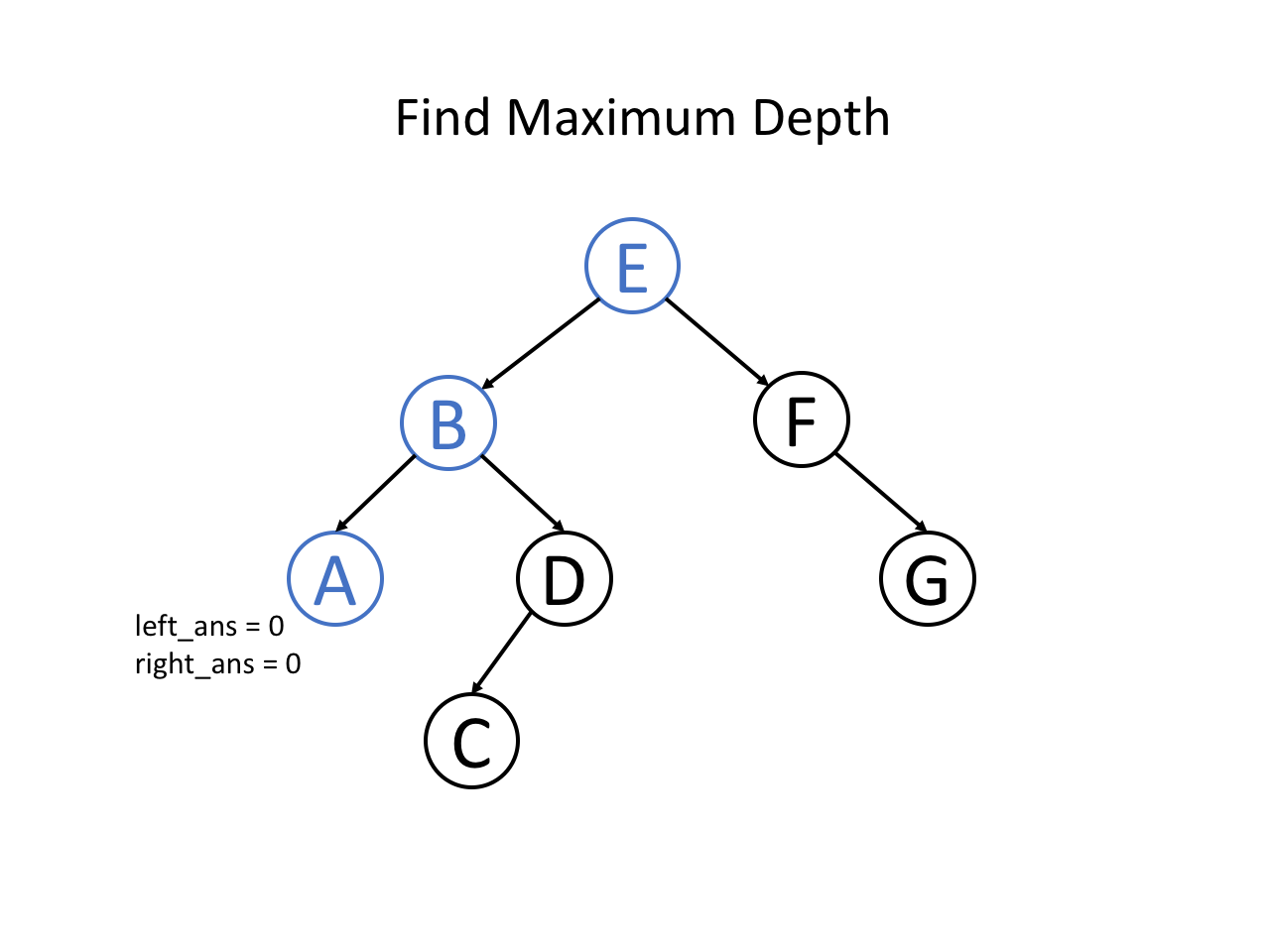
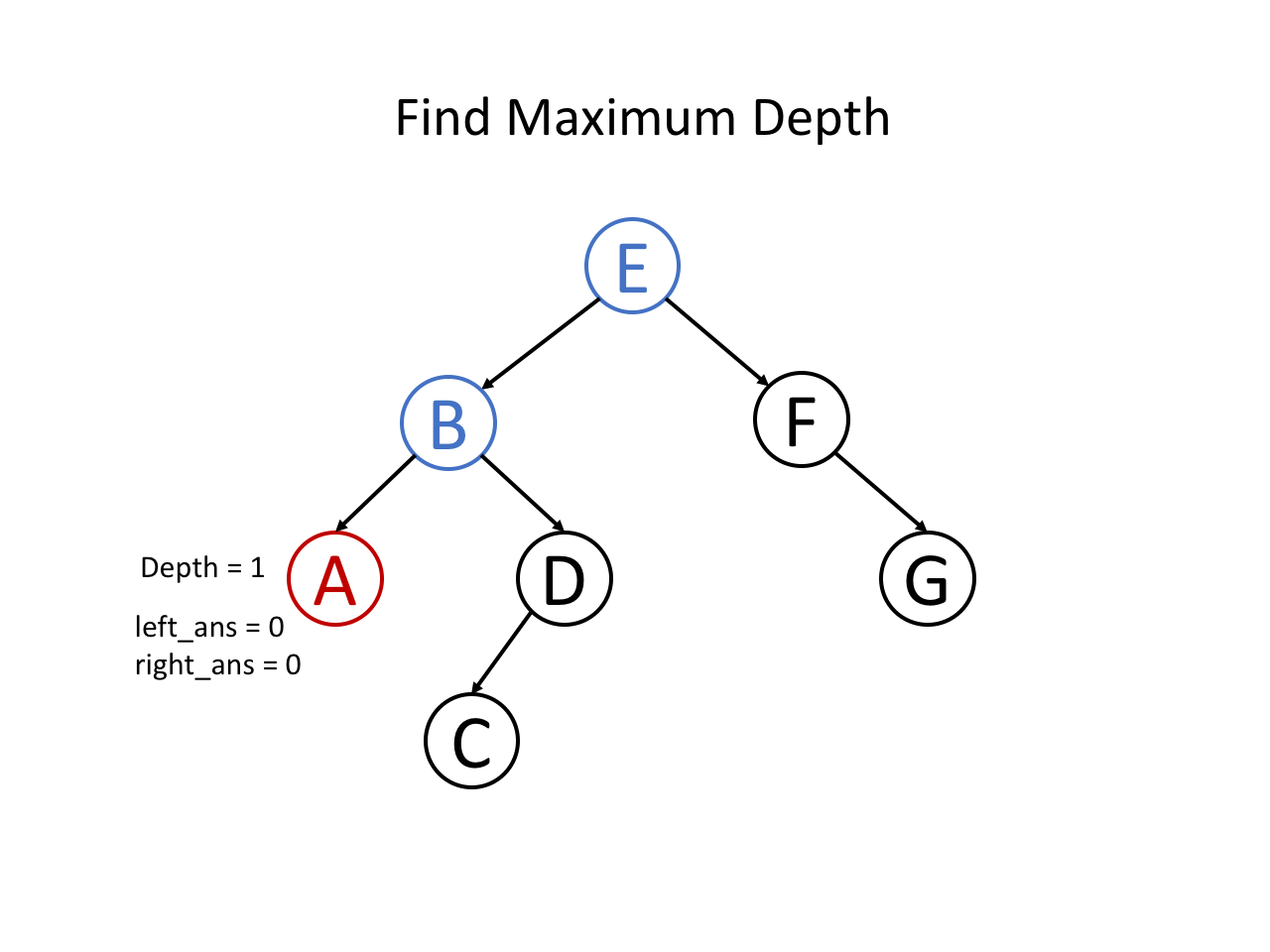
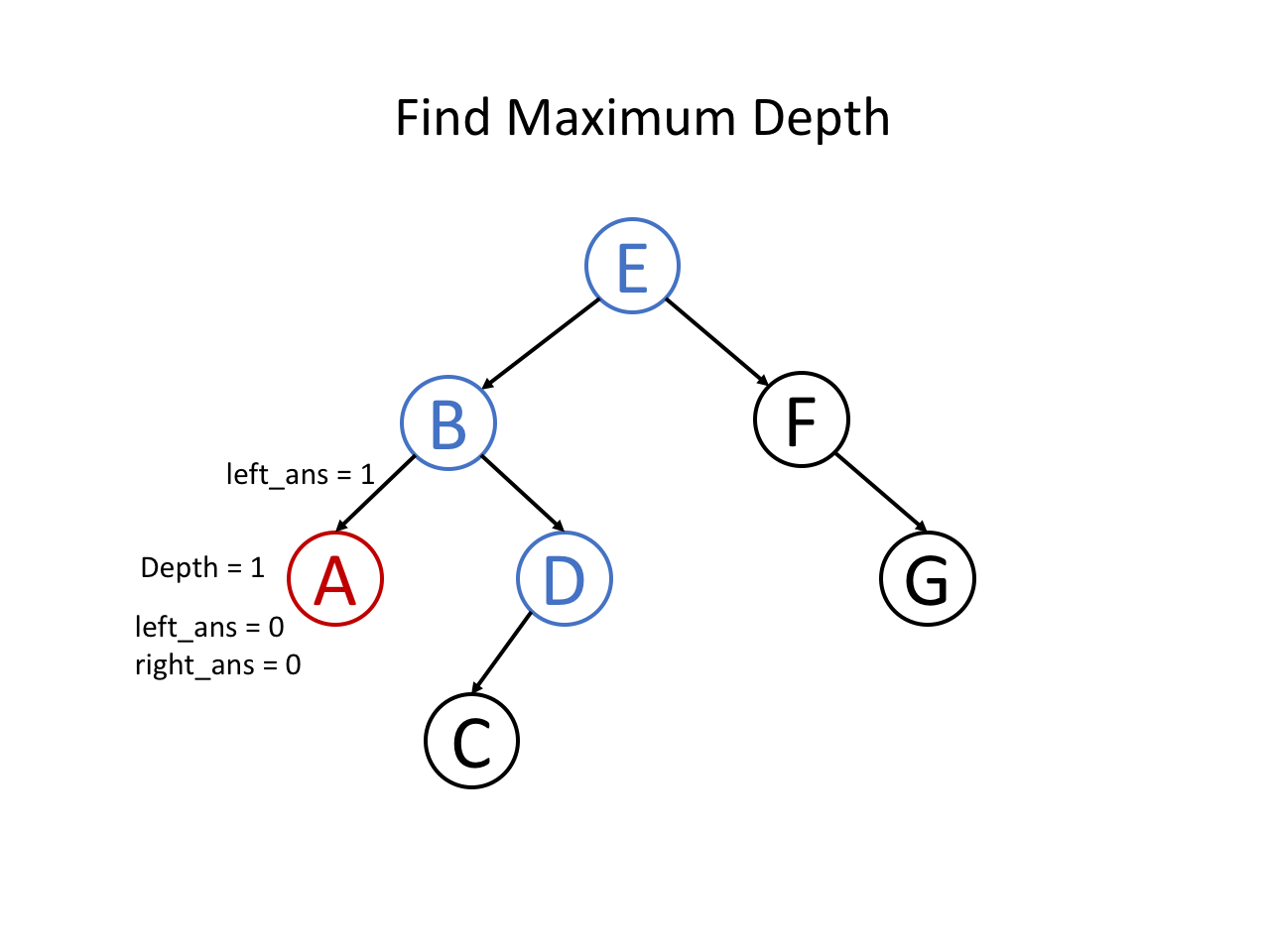
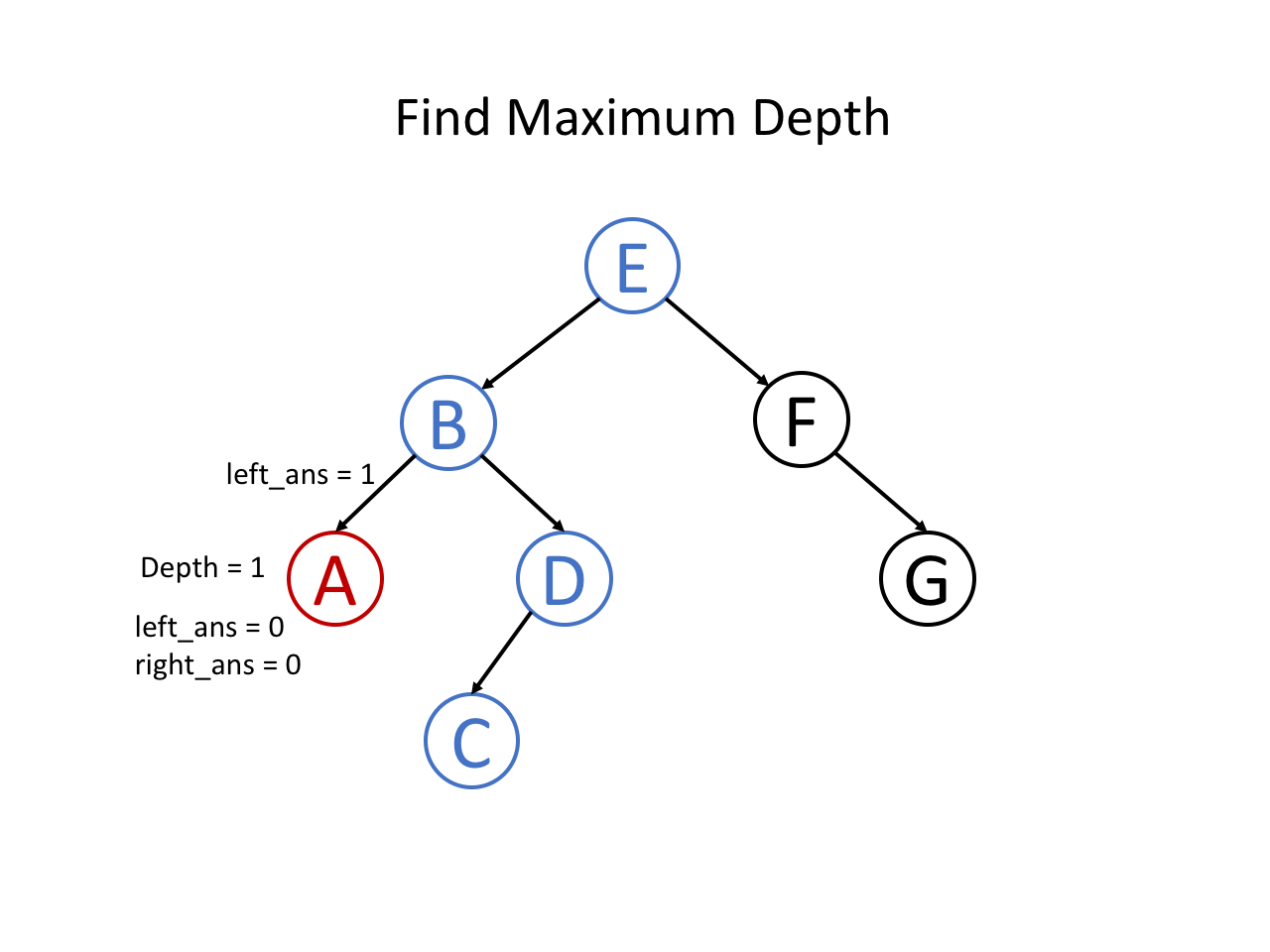
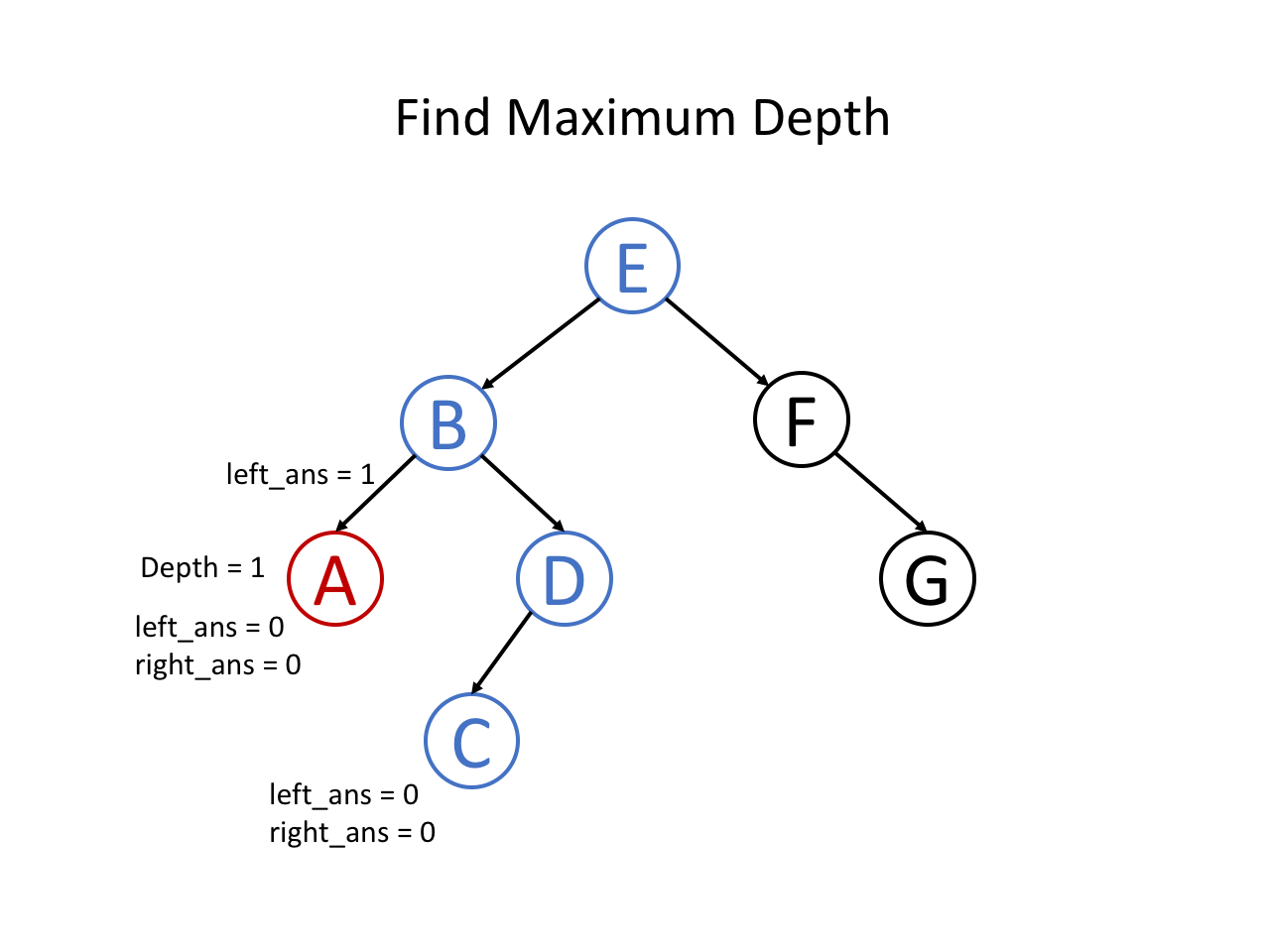
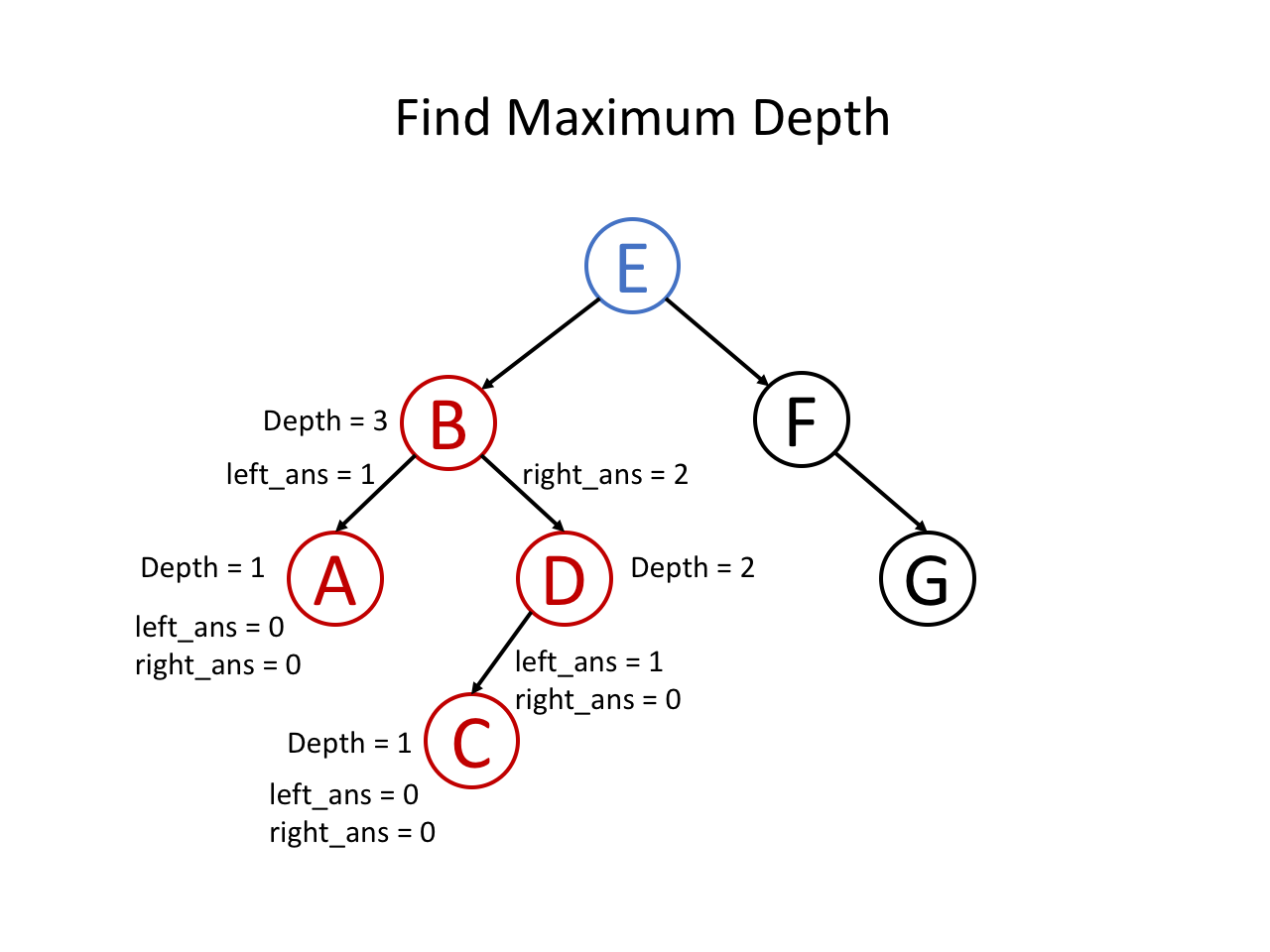
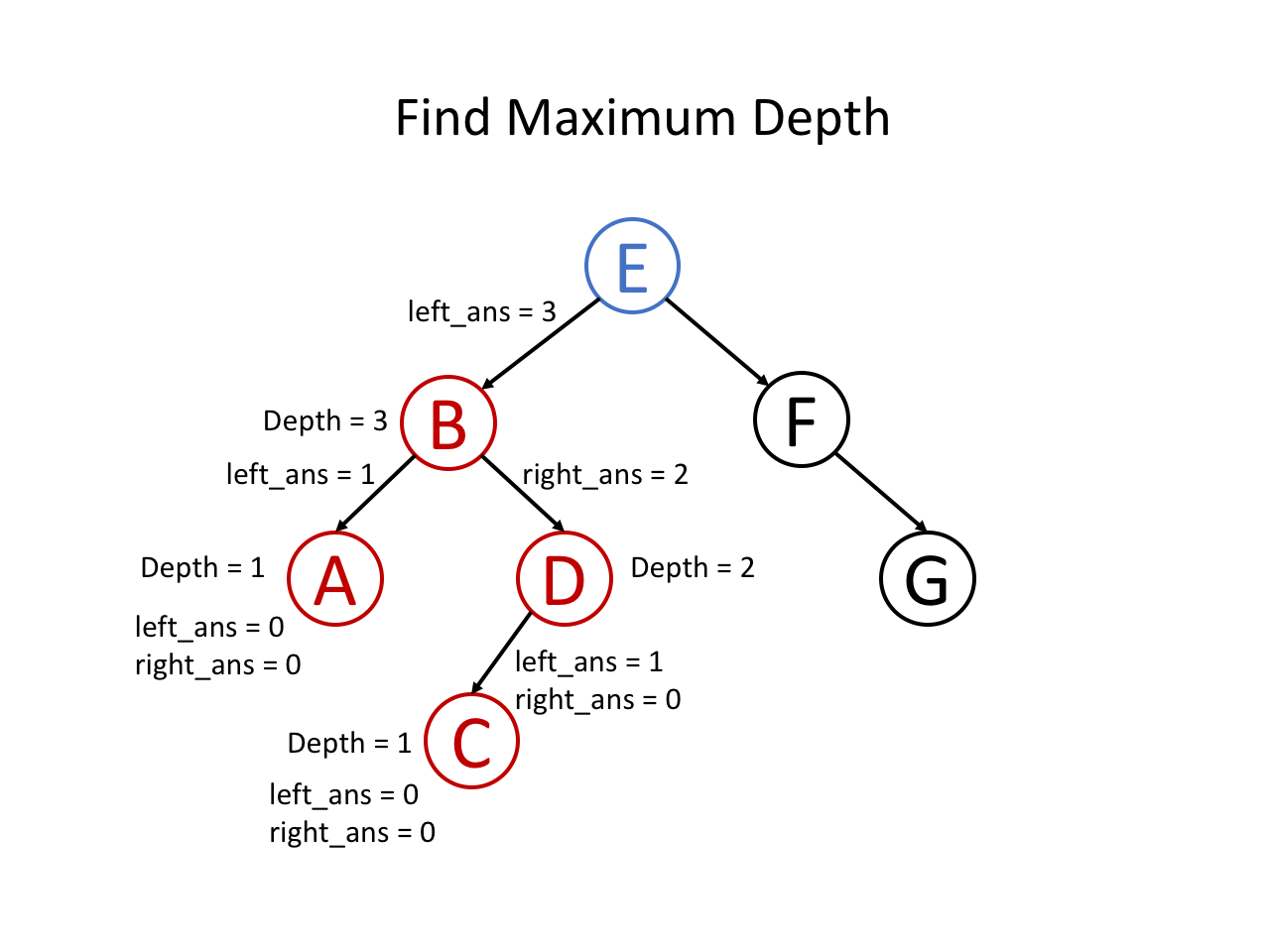
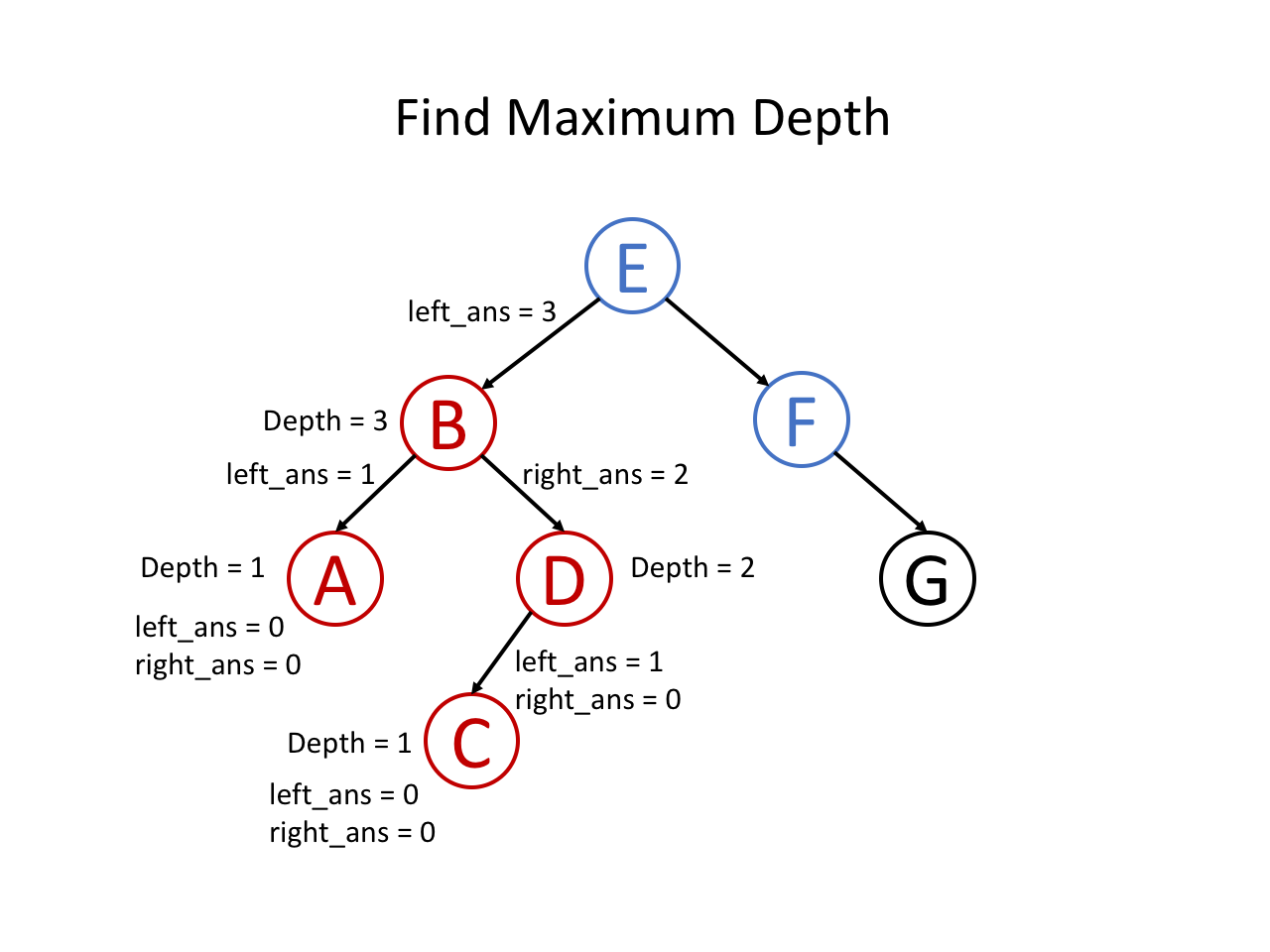
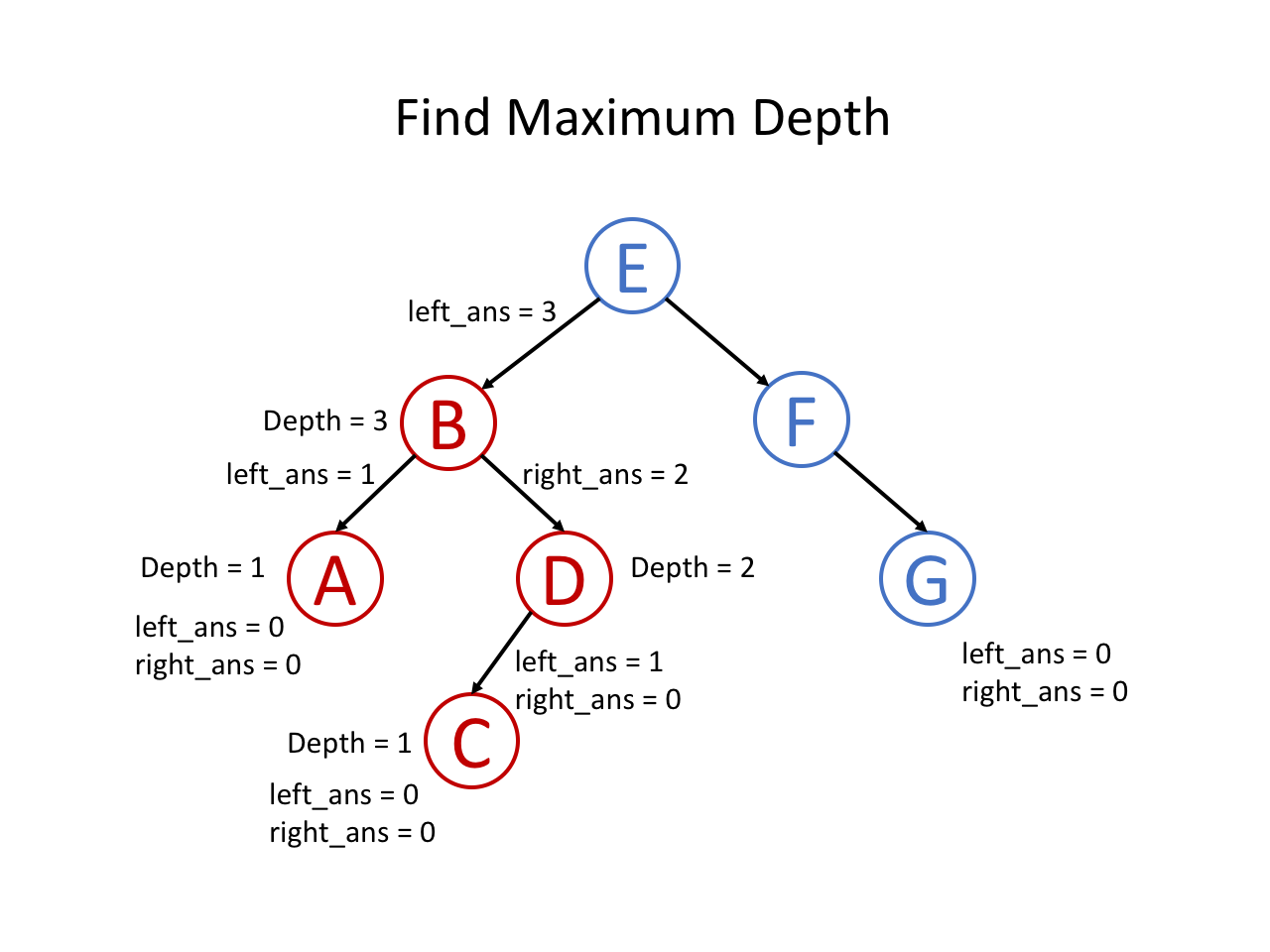
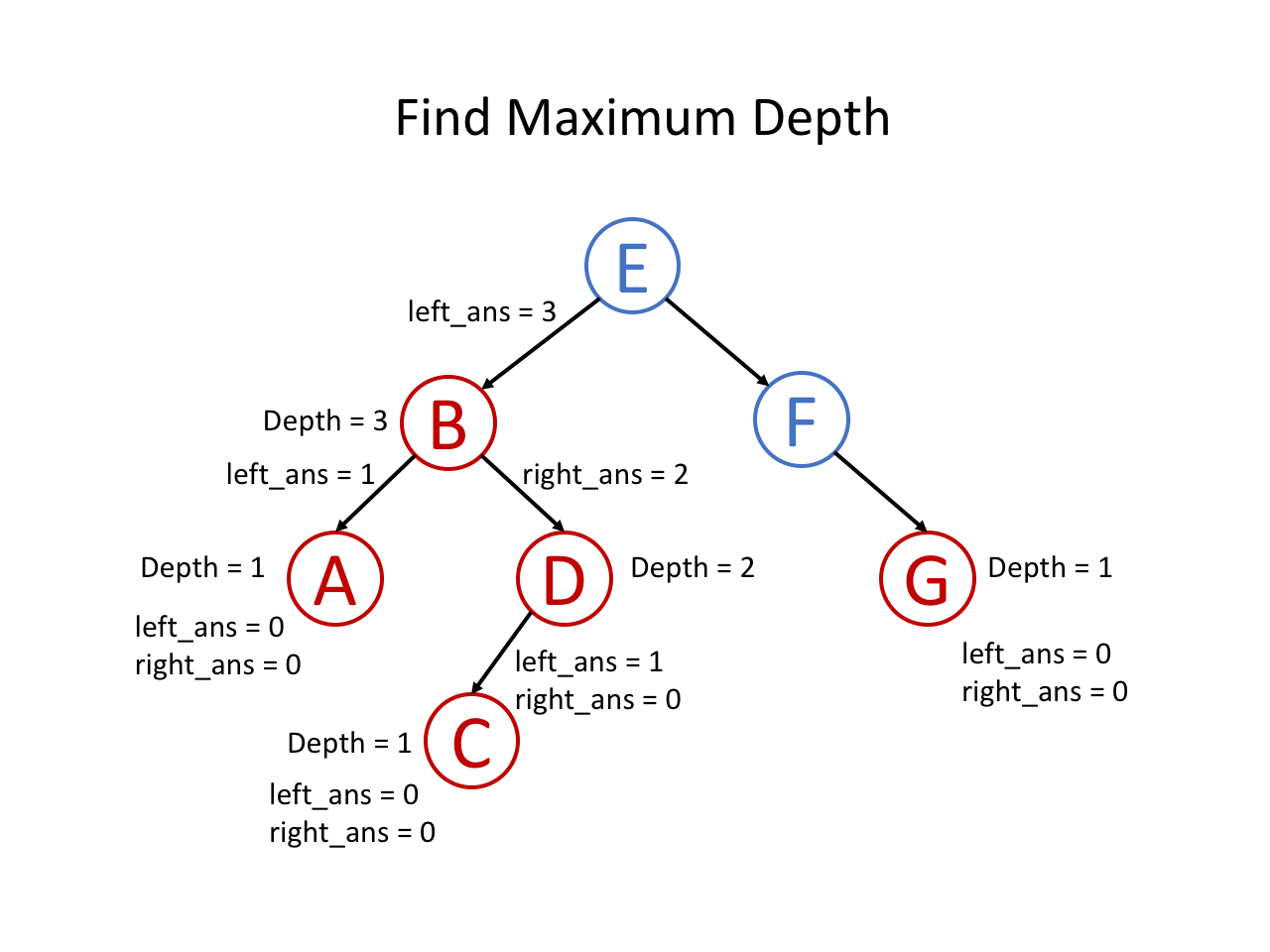
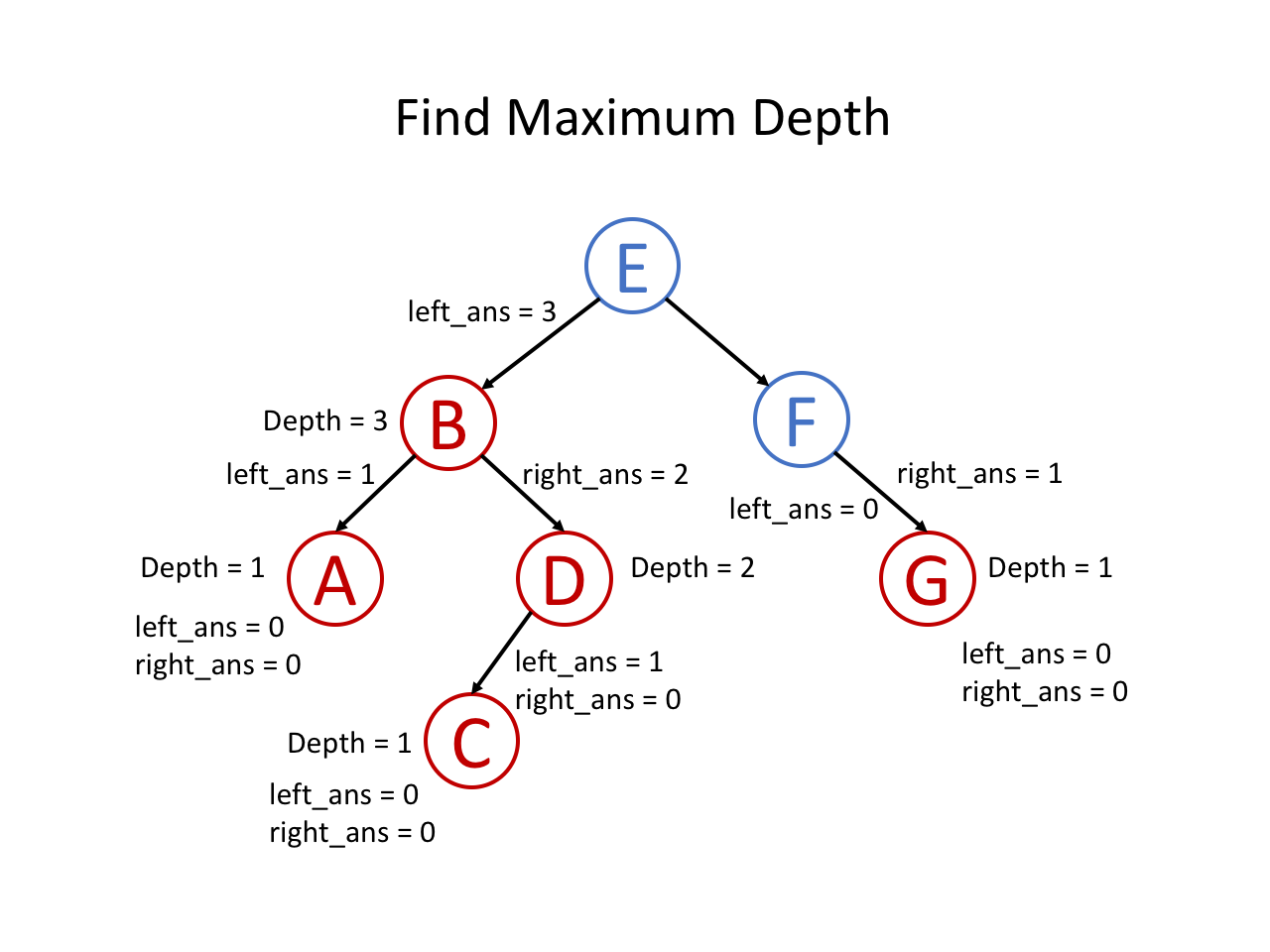
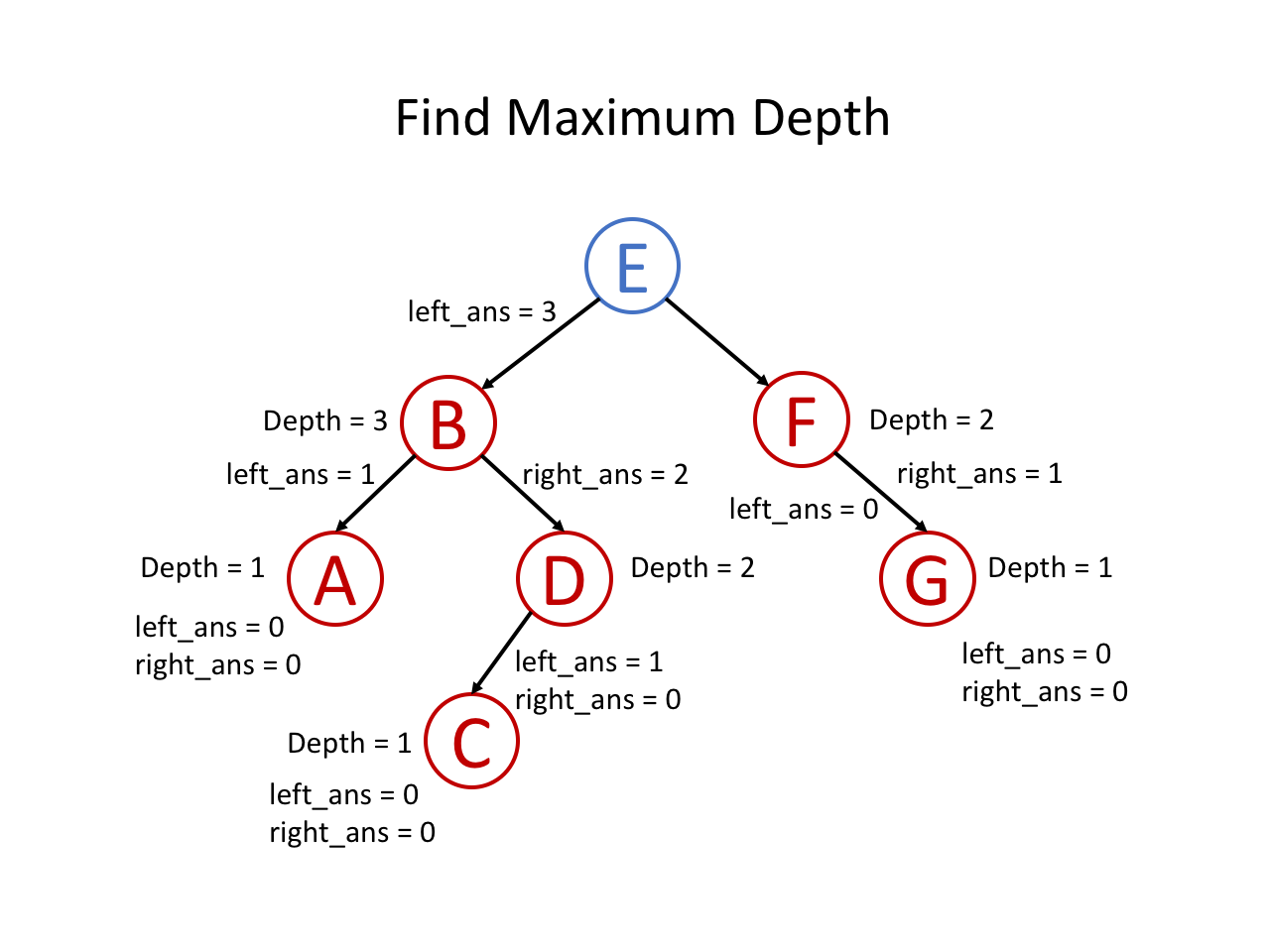
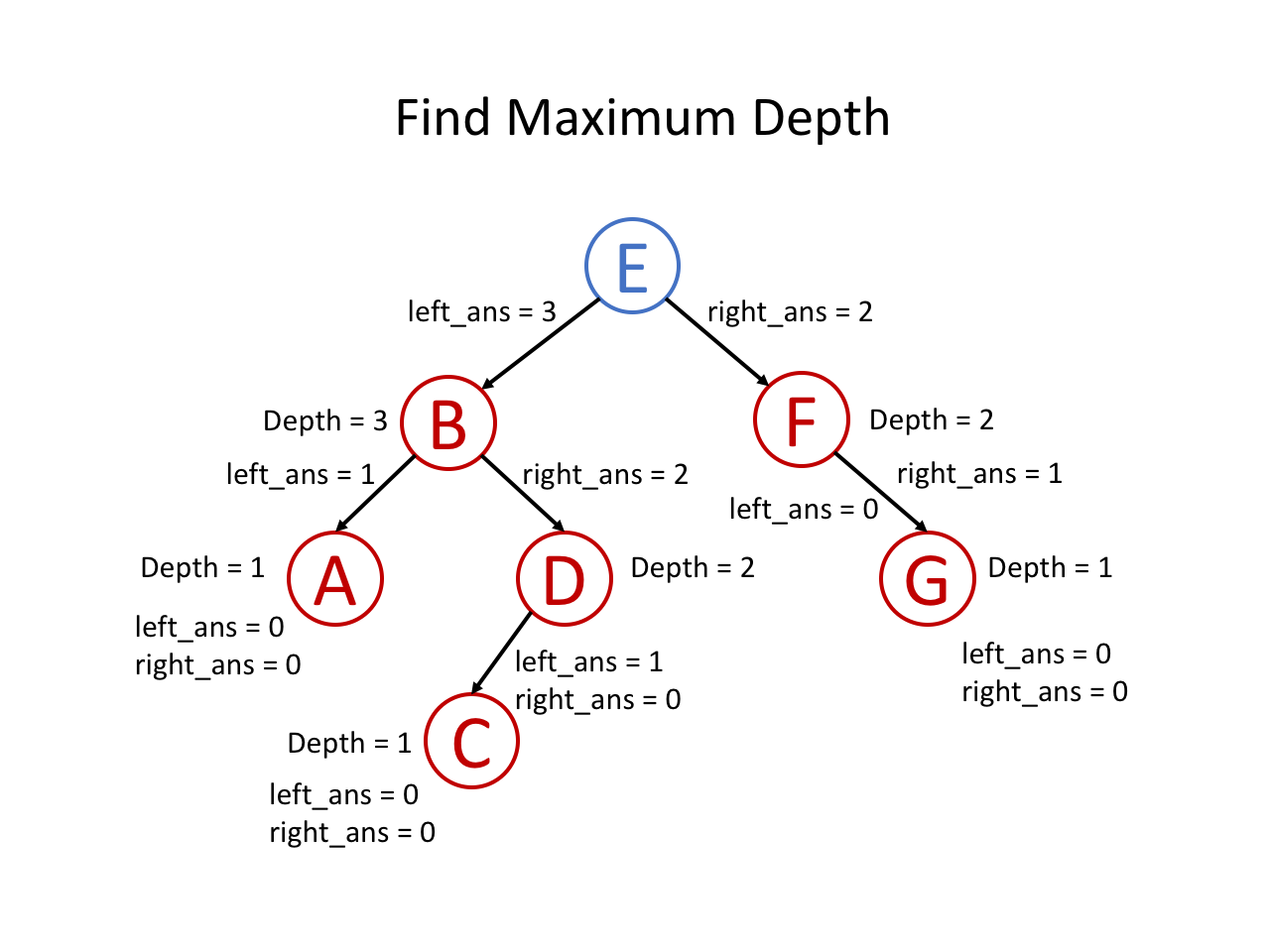
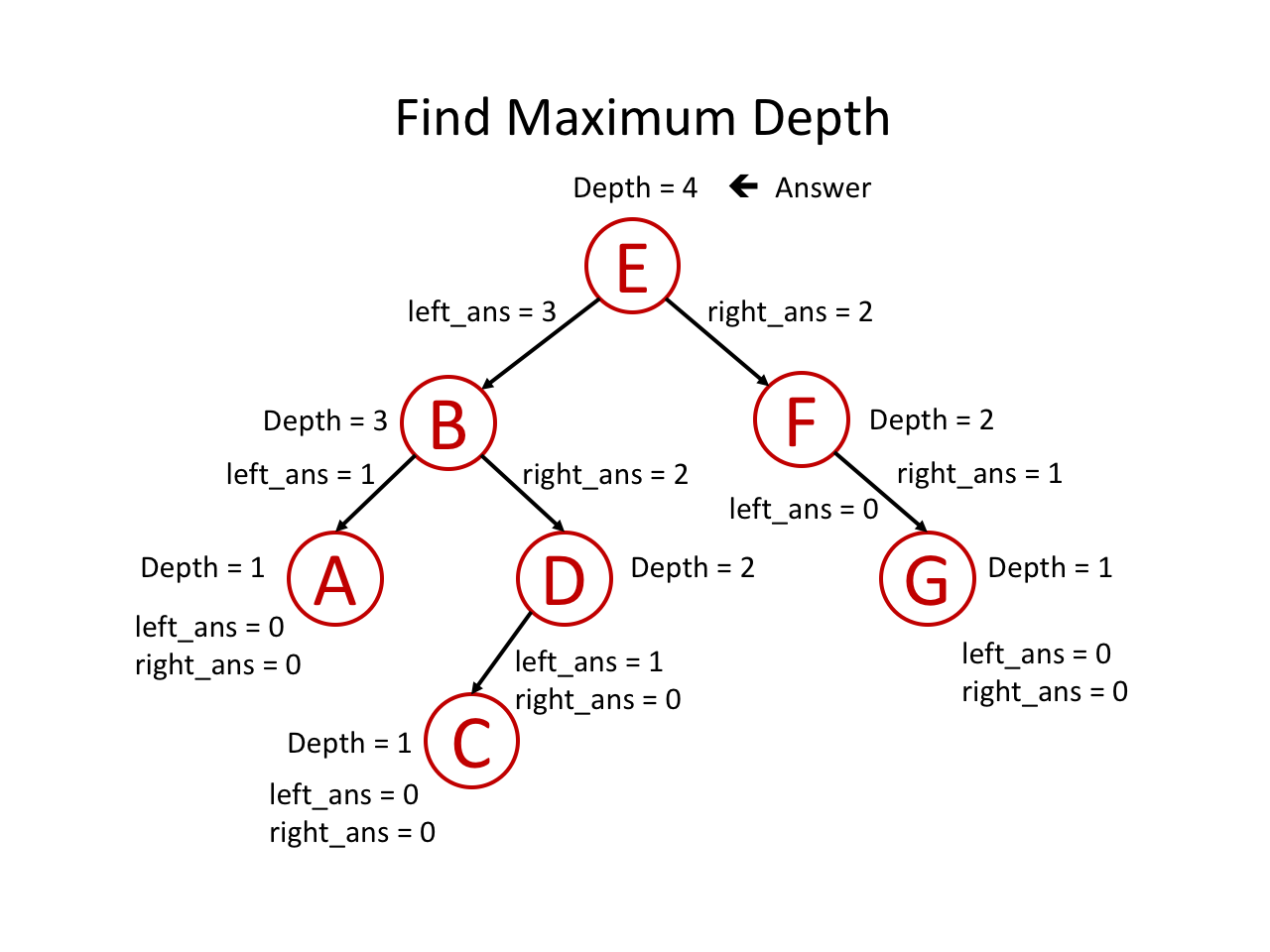
整个过程可以参考如下幻灯片：

pic
1 / 12

自底向上思路​

下面我们继续讨论前面关于树的最大深度问题，但是这次使用 “自底向上” 的思路。

划分子问题​

如果想要知道整棵树以 root 为根节点的最大深度是多少，那么就需要知道：

  • 以 root.left 为根节点的最大深度是多少
  • 以 root.right 为根节点的最大深度是多少

最后取 max(leftDepth, rightDepth) + 1 即左子树和右子树的最大深度中大的那一个，然后再加上 root 本身。

这里划分的子问题就是，对于树的单个节点，以节点自身为根的子树的最大深度 x 是多少。

清楚自底向上的递归返回过程​

整个递归的返回过程是先从最左边叶子节点开始，一层层往上返回的，每到一颗子树，都会先递归到其最左边的叶子子节点，接着一层层返回到根节点，接着递归右子树。

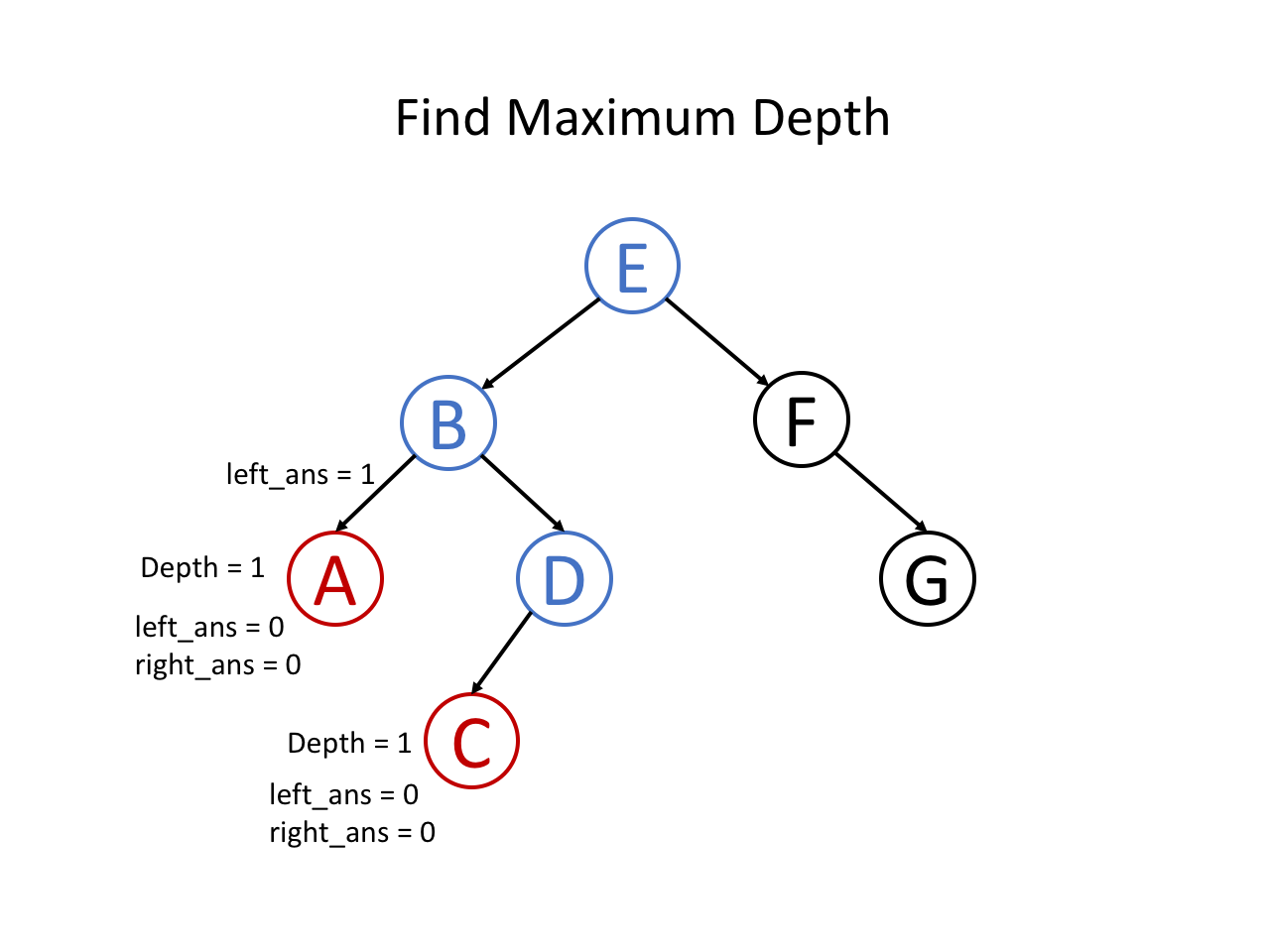
具体可以参考下面的幻灯片：

pic
1 / 25

整个过程就是二叉树的后序遍历：

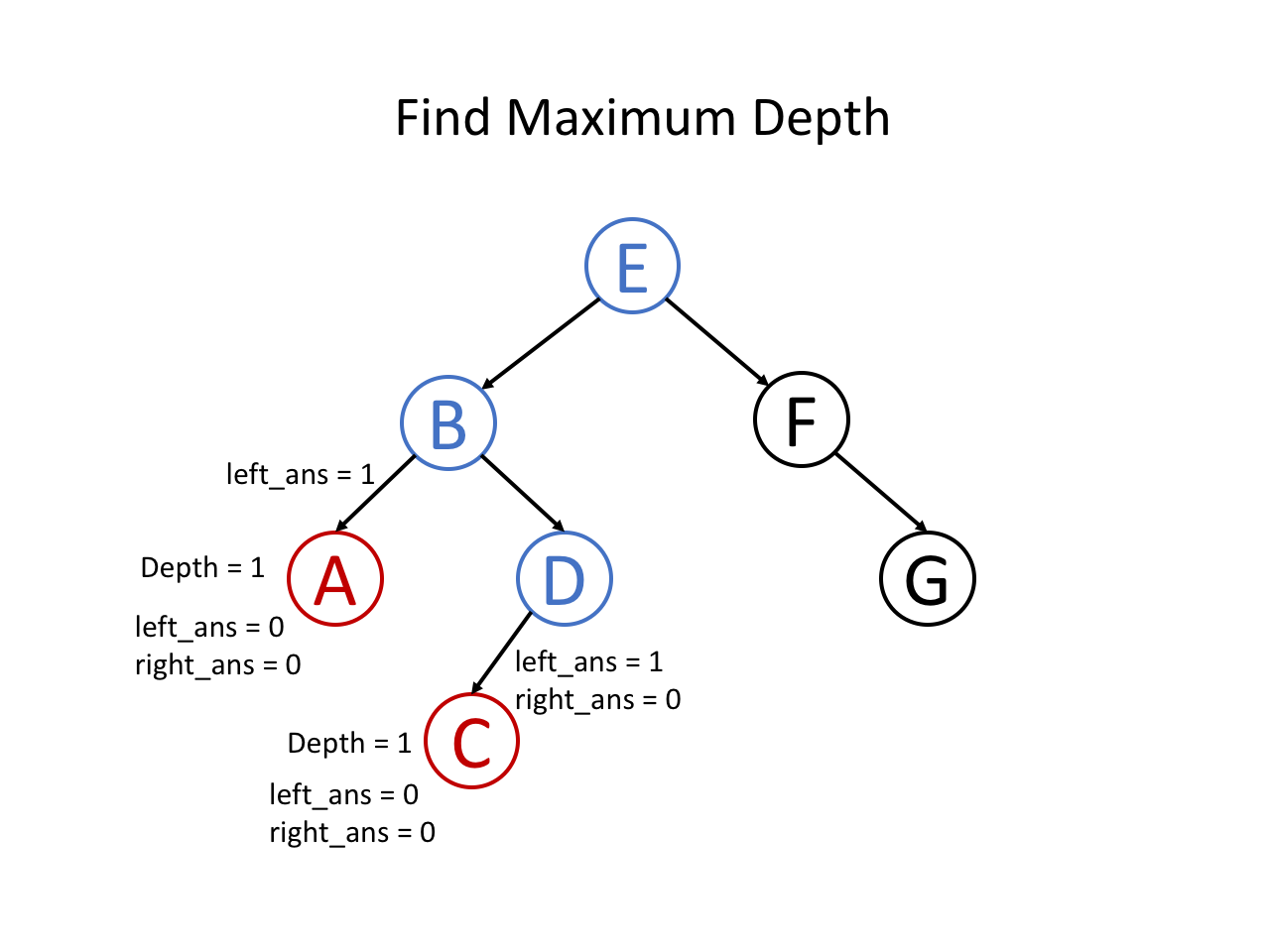
  • 首先会深入递归到二叉树最左边的叶子节点，以该叶子节点为根节点，计算它的最大深度（为 1）
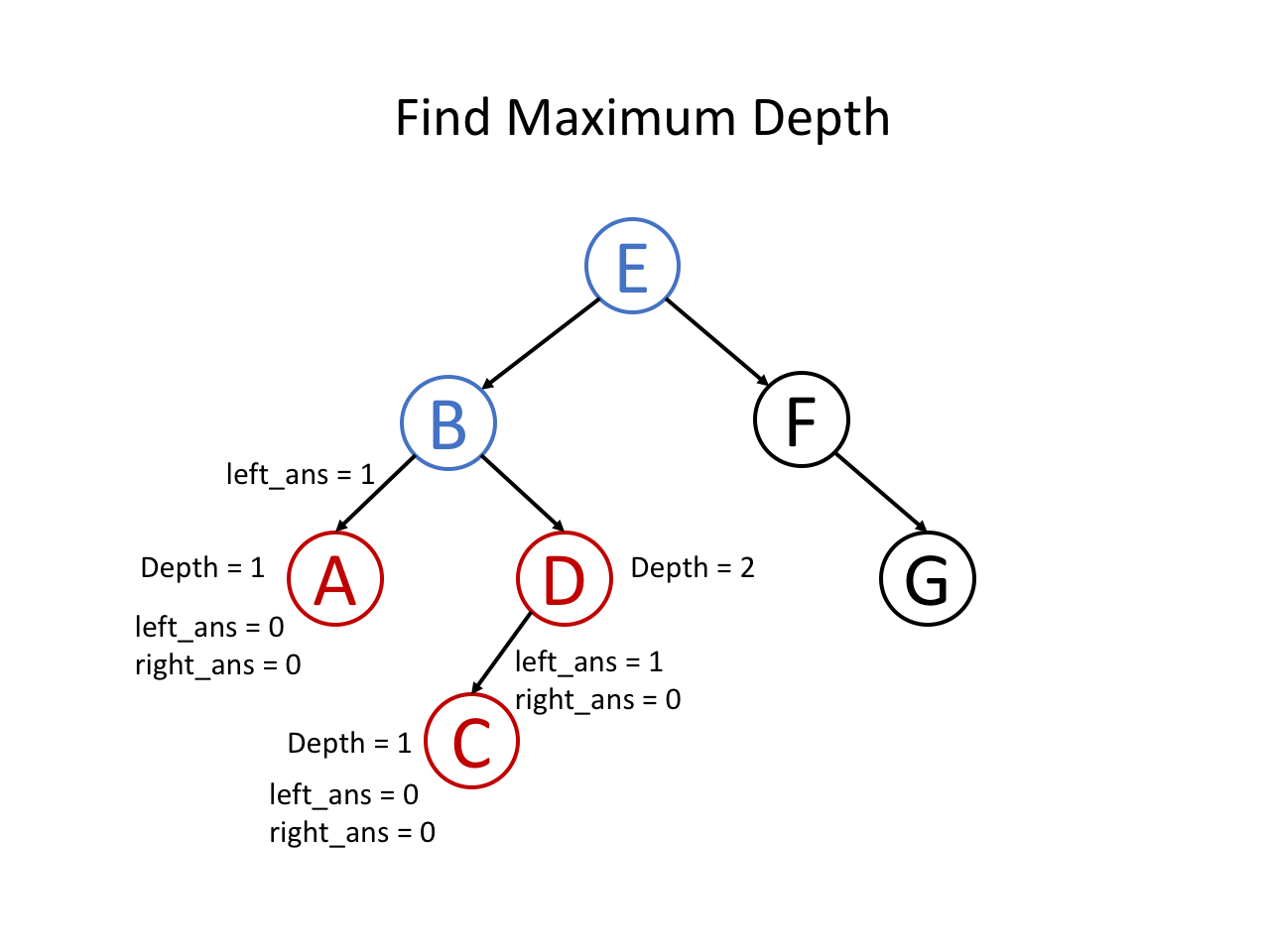
  • 然后回溯到该叶子节点的父节点，接着递归到右节点，以该叶子节点为根节点，计算它的最大深度（为 1）
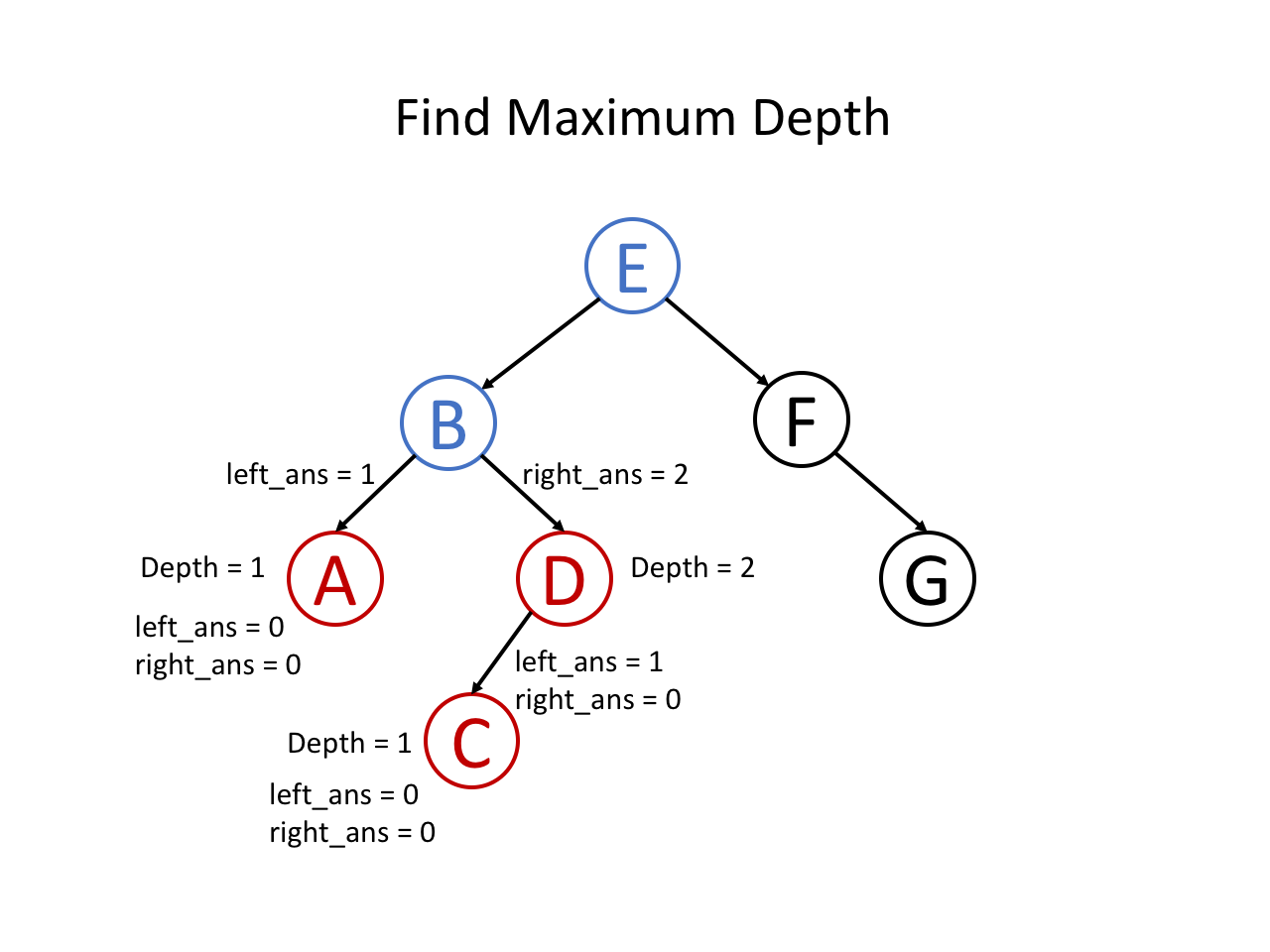
  • 左右两个子节点都递归完后，以倒数第二层的该节点为根节点，计算它的最大深度（为 2）
  • ...最终会递归完根节点的左子树、右子树，最后返回层度最深的那个，再加上根节点本身（+1）
function maxDepth(root) {
  if (!root) return;

  let leftDepth = maxDepth(root.left);
  let rightDepth = maxDepth(root.right);

  return Math.max(leftDepth, rightDepth) + 1;
}

总结​

自顶向下​

当遇到树问题时，请先思考一下两个问题：

你能确定一些参数，从该节点自身解决出发寻找答案吗？ 你可以使用这些参数和节点本身的值来决定什么应该是传递给它子节点的参数吗？ 如果答案都是肯定的，那么请尝试使用 “自顶向下” 的递归来解决此问题。

  • 自顶向下的递归可读性不好，但是对于每层递归做了什么事情其实很好分析
  • 自底向上的整个过程就是二叉树的前序遍历，从叶子节点开始一层层往下递归，一般会有一个外部变量用来记录每层递归更新的答案

自底向上​

对于树中的任意一个节点，如果你知道它子节点的答案，你能计算出该节点的答案吗？ 如果答案是肯定的，那么 “自底向上” 的递归可能是一个不错的解决方法。

  • 自底向上的递归可读性更高，但是对于每层递归做了什么事情不是很好分析
  • 自底向上的整个过程就是二叉树的后序遍历，从解决叶子节点的问题开始，解决一个个子问题，最终解决整个大问题
  • 不需要外部变量保存答案，因为后序遍历最后一次递归函数返回是在根节点的位置，所以自底向上的递归函数最后一行必须有明确的返回值

Reference​